Question

4．如图，在正方体ABCD-A₁B₁C₁D₁，若E是AD的中点，则异面直线A₁B与C₁E所成角等于90°

Answer 1

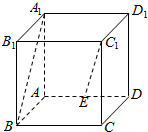
分析 以A为原点，AB为x轴，AD为y轴，AA₁为z轴，建立空间直角坐标系，利用向量法能求出异面直线A₁B与C₁E所成角．

解答 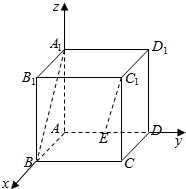解：以A为原点，AB为x轴，AD为y轴，AA₁为z轴，建立空间直角坐标系，
设正方体ABCD-A₁B₁C₁D₁的棱长为2，
则A₁（0，0，2），B（2，0，0），C₁（2，2，2），E（0，1，0），
$\overrightarrow{{{A}_{1}B}^{\;}}$=（2，0，-2），$\overrightarrow{{C}_{1}E}$=（-2，-1，-2），
设异面直线A₁B与C₁E所成角为θ，
则cosθ=$\frac{|\overrightarrow{{A}_{1}B}•\overrightarrow{{C}_{1}E}|}{|\overrightarrow{{A}_{1}B}|•|\overrightarrow{{C}_{1}E}|}$=$\frac{|-4+4|}{\sqrt{8}•\sqrt{9}}$=0，
∴θ=90°．
∴异面直线A₁B与C₁E所成角等于90°．
故答案为：90°．

点评 本题考查异面直线所成角的求法，是基础题，解题时要认真审题，注意向量法的合理运用．