
分析 (1)求出f(x)的导数,可得切线的斜率和切点,由点斜式方程即可得到所求方程;
(2)求出f(x)的导数,再令g(x)=f′(x),求出g(x)的导数,可得g(x)在区间[0,$\frac{π}{2}$]的单调性,即可得到f(x)的单调性,进而得到f(x)的最值.
解答 解:(1)函数f(x)=excosx-x的导数为f′(x)=ex(cosx-sinx)-1,
可得曲线y=f(x)在点(0,f(0))处的切线斜率为k=e0(cos0-sin0)-1=0,
切点为(0,e0cos0-0),即为(0,1),
曲线y=f(x)在点(0,f(0))处的切线方程为y=1;
(2)函数f(x)=excosx-x的导数为f′(x)=ex(cosx-sinx)-1,
令g(x)=ex(cosx-sinx)-1,
则g(x)的导数为g′(x)=ex(cosx-sinx-sinx-cosx)=-2ex•sinx,
当x∈[0,$\frac{π}{2}$],可得g′(x)=-2ex•sinx≤0,
即有g(x)在[0,$\frac{π}{2}$]递减,可得g(x)≤g(0)=0,
则f(x)在[0,$\frac{π}{2}$]递减,
即有函数f(x)在区间[0,$\frac{π}{2}$]上的最大值为f(0)=e0cos0-0=1;
最小值为f($\frac{π}{2}$)=e${\;}^{\frac{π}{2}}$cos$\frac{π}{2}$-$\frac{π}{2}$=-$\frac{π}{2}$.
点评 本题考查导数的运用:求切线的方程和单调区间、最值,考查化简整理的运算能力,正确求导和运用二次求导是解题的关键,属于中档题.


科目:高中数学 来源: 题型:解答题
| 最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
| 天数 | 2 | 16 | 36 | 25 | 7 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
| 天数 | 2 | 16 | 36 | 25 | 7 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
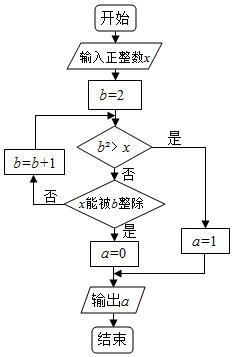 执行两次如图所示的程序框图,若第一次输入的x值为7,第二次输入的x值为9,则第一次,第二次输出的a值分别为( )
执行两次如图所示的程序框图,若第一次输入的x值为7,第二次输入的x值为9,则第一次,第二次输出的a值分别为( )| A. | 0,0 | B. | 1,1 | C. | 0,1 | D. | 1,0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com