
���� �����������֪����$\overrightarrow{PQ}=\frac{3}{2}\overrightarrow{QB}$�����Q�����꣬���������ԲE�ķ��̣�
������ֱ��y=kx-2��������Բ���̣���Τ�ﶨ�����ɡ���0��������ԭ��Oλ����MNΪֱ����Բ�⣬��$\overrightarrow{OM}•\overrightarrow{ON}��0$�������������������깫ʽ���������ֱ��lб�ʵ�ȡֵ��Χ��
��� �⣺����������֪����ABP�ǵ���ֱ�������Σ�a=2��B��2��0����
��Q��x0��y0������$\overrightarrow{PQ}=\frac{3}{2}\overrightarrow{QB}$����${x_0}=\frac{6}{5}��{y_0}=-\frac{4}{5}$��
������Բ���̣����b2=1��
����Բ����Ϊ$\frac{x^2}{4}+{y^2}=1$������5�֣�
�����������֪��ֱ��l��б�ʴ��ڣ�����Ϊy=kx-2����M��x1��y1����N��x2��y2����
��$\left\{\begin{array}{l}y=kx-2\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$���������1+4k2��x2-16kx+12=0��
��Τ�ﶨ����֪��x1+x2=$\frac{16k}{{1+4{k^2}}}$��x1x2=$\frac{12}{{1+4{k^2}}}$������8�֣�
��ֱ��l��E��������ͬ�Ľ��㣬�����0��
����-16k��2-4��12����1+4k2����0����ã�k2��$\frac{3}{4}$�����١���9�֣�
������ԭ��Oλ����MNΪֱ����Բ�⣬��$\overrightarrow{OM}•\overrightarrow{ON}��0$����x1x2+y1y2��0��
��x1x2+y1y2=x1x2+��kx1-2����kx2-2��
=��1+k2��x1x2-2k����x1+x2��+4
=��1+k2��$\frac{12}{{1+4{k^2}}}$-2k��$\frac{16k}{{1+4{k^2}}}$+4��0��
��ã�k2��4�����ڡ���11�֣�
�ۺϢ٢ڿ�֪��$\frac{3}{4}$��k2��4�����$\frac{{\sqrt{3}}}{2}$��k��2��-2��k��-$\frac{{\sqrt{3}}}{2}$��
ֱ��lб�ʵ�ȡֵ��Χ��-2��-$\frac{{\sqrt{3}}}{2}$���ȣ�$\frac{{\sqrt{3}}}{2}$��2��������12�֣�
���� ���⿼����Բ�ı����̼��������ʣ�����ֱ������Բ��λ�ù�ϵ�������������������������㣬Τ�ﶨ�������鼰�������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
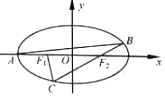 ��ͼ�����A��F1��F2�ֱ�Ϊ��Բ$\frac{x^2}{4}+\frac{y^2}{3}=1$��������ҽ��㣬����A��б��Ϊk��ֱ�߽���Բ����һ��B������BF2���ӳ�����Բ�ڵ�C��
��ͼ�����A��F1��F2�ֱ�Ϊ��Բ$\frac{x^2}{4}+\frac{y^2}{3}=1$��������ҽ��㣬����A��б��Ϊk��ֱ�߽���Բ����һ��B������BF2���ӳ�����Բ�ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
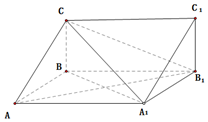 ��ͼ��������ABC-A1B1C1�У��ı���AA1BB1�����Σ���BB1A1=$\frac{��}{3}��{C_1}{B_1}����A{A_1}B{B_1}$�������C-A1B1-BΪ$\frac{��}{6}$��CB=1��
��ͼ��������ABC-A1B1C1�У��ı���AA1BB1�����Σ���BB1A1=$\frac{��}{3}��{C_1}{B_1}����A{A_1}B{B_1}$�������C-A1B1-BΪ$\frac{��}{6}$��CB=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1-3i}{5}$ | B�� | $\frac{1+3i}{5}$ | C�� | $\frac{3+i}{5}$ | D�� | $\frac{3-i}{5}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com