
 如图,在正三棱锥P-ABC中,D,E分别是AB,AC的中点,O为顶点P在底面ABC内的投影,有下列三个论断:①AC⊥PB;②AC∥平面POD;③AB⊥平面POD,其中正确论断的个数为( )
如图,在正三棱锥P-ABC中,D,E分别是AB,AC的中点,O为顶点P在底面ABC内的投影,有下列三个论断:①AC⊥PB;②AC∥平面POD;③AB⊥平面POD,其中正确论断的个数为( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
分析 由P-ABC是正三棱锥,可知底面△ABC是正三角形,且顶点P在底面ABC内的投影O是底面三角形的中心,然后利用线面垂直的判定可得AC⊥平面PBE,AB⊥平面POD,可知①③正确;由AC∩平面POD=C知②错误.
解答 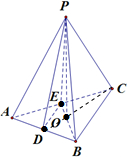 解:∵P-ABC是正三棱锥,∴底面△ABC是正三角形,
解:∵P-ABC是正三棱锥,∴底面△ABC是正三角形,
且顶点P在底面ABC内的投影O是底面三角形的中心,
又D,E分别是AB,AC的中点,则BE∩CD于O,且BE⊥AC,CD⊥AB.
又PO⊥底面ABC,∴PO⊥AC,PO⊥AB,则AC⊥平面PBE,
有AC⊥PB,故①正确;
AB⊥平面PCD,即AB⊥平面POD,故③正确;
AC∩平面POD=C,故②错误.
∴正确论断的个数为2个.
故选:B.
点评 本题考查棱锥的结构特征,考查了线面垂直的判定和性质,考查空间想象能力和思维能力,是中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {y|$\frac{1}{2}$<y<1} | B. | {y|0<y$<\frac{1}{2}$} | C. | ∅ | D. | {y|0<y<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (-1,0)∪(3,4) | C. | (3,4) | D. | [0,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 明天上午下雨,下午不下雨 | |
| B. | 明天下雨的概率为80% | |
| C. | 明天有的地方下雨,有的地方不下雨 | |
| D. | 明天下雨的时间一共是19.2小时 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com