
分析 先联立方程,组成方程组,求得交点坐标,可得被积区间,再用定积分表示出曲线y=x2与直线y=6x围成的封闭图形的面积,即可求得结论.
解答 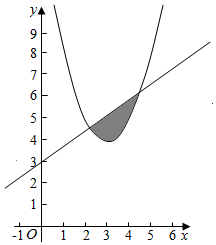 解:联立方程得$\left\{\begin{array}{l}{y=x+3}\\{y={x}^{2}-6x+13}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$或$\left\{\begin{array}{l}{x=5}\\{y=8}\end{array}\right.$,
解:联立方程得$\left\{\begin{array}{l}{y=x+3}\\{y={x}^{2}-6x+13}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$或$\left\{\begin{array}{l}{x=5}\\{y=8}\end{array}\right.$,
∴直线y=x+3和曲线y=x2-6x+13围成的封闭图形的面积为:
${∫}_{2}^{5}$[(x+3)-(x2-6x+13)]dx=${∫}_{2}^{5}$(-x2+7x-10)dx=(-$\frac{1}{3}$x3+$\frac{7}{2}$x2-10x)|${\;}_{2}^{5}$=$\frac{9}{2}$
故答案为:$\frac{9}{2}$
点评 本题考查利用定积分求面积,解题的关键是确定被积区间及被积函数.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 2π | C. | π | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AD}$ | B. | 2$\overrightarrow{AD}$ | C. | 3$\overrightarrow{AD}$ | D. | 4$\overrightarrow{AD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 30°或150° | C. | 45° | D. | 45°或135° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com