
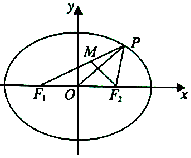
 如图所示,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,其中a>b>0,F1,F2分别为其左,右焦点,点P是椭圆C上一点,PO⊥F2M,且$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$.
如图所示,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,其中a>b>0,F1,F2分别为其左,右焦点,点P是椭圆C上一点,PO⊥F2M,且$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$.分析 (1)当$a=2\sqrt{2}$,b=2时,椭圆C为:$\frac{x^2}{8}+\frac{y^2}{4}=1$,可得F1,F2,利用PF2⊥F1F2,可得P坐标.可得直线F2M方程,直线F1M方程,解得λ.
(2)设P(x0,y0),M(xM,yM),由$\overrightarrow{{F_1}M}=2\overrightarrow{MP}$,可得$\overrightarrow{{F}_{1}M}$,M坐标,$\overrightarrow{{F}_{2}M}$,由$\overrightarrow{PO}⊥\overrightarrow{{F_2}M}$,$\overrightarrow{OP}=({x_0},{y_0})$,又$\frac{{{x_0}^2}}{a^2}+\frac{{{y_0}^2}}{b^2}=1$,联立解出即可得出.
解答 解:(1)当$a=2\sqrt{2}$,b=2时,椭圆C为:$\frac{x^2}{8}+\frac{y^2}{4}=1$,F1(-2,0),F2(2,0),
∴PF2⊥F1F2,则$P(2,\sqrt{2})$或$P(2,-\sqrt{2})$,
当$P(2,\sqrt{2})$时,${k_{OP}}=\frac{{\sqrt{2}}}{2}$,${k_{{F_2}M}}=-\sqrt{2}$,${k_{{F_1}M}}=\frac{{\sqrt{2}}}{4}$,
直线F2M:$y=-\sqrt{2}(x-2)$,①
直线F1M:$y=\frac{{\sqrt{2}}}{4}(x+2)$,②
联立①②解得${x_1}=\frac{6}{5}$,
∴$λ=\frac{{{x_M}-{x_{F_1}}}}{{{x_P}-{x_M}}}=4$.
同理可得当$P(2,-\sqrt{2})$时,λ=4,
综上所述,λ=4.
(2)设P(x0,y0),M(xM,yM),
由$\overrightarrow{{F_1}M}=2\overrightarrow{MP}$,
∴$\overrightarrow{{F_1}M}=\frac{2}{3}({x_0}+c,{y_0})=({x_M}+c,{y_M})$,
∴$M(\frac{2}{3}{x_0}-\frac{1}{3}c,\frac{2}{3}{y_0})$,$\overrightarrow{{F_2}M}=(\frac{2}{3}{x_0}-\frac{4}{3}c,\frac{2}{3}{y_0})$,
由$\overrightarrow{PO}⊥\overrightarrow{{F_2}M}$,$\overrightarrow{OP}=({x_0},{y_0})$,
∴$(\frac{2}{3}{x_0}-\frac{4}{3}c){x_0}+\frac{2}{3}{y_0}^2=0$,
即${x_0}^2+{y_0}^2=2c{x_0}$,③
又$\frac{{{x_0}^2}}{a^2}+\frac{{{y_0}^2}}{b^2}=1$,④
联立③④解得${x_0}=\frac{a+c}{c}$(舍)或${x_0}=\frac{a(a-c)}{c}$,(∵x0∈(-a,a)),
∴${x_0}=\frac{a(a-c)}{c}∈(0,a)$,即0<a2-ac<ac,
∴$e>\frac{1}{2}$,故$e∈(\frac{1}{2},1)$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、向量运算性质、不等式解法,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 超市 | A | B | C | D | E | F | G |
| 广告费支出xi | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
| 销售额yi | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 4 | C. | 0 | D. | 5-e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$=$\overrightarrow{0}$,$\overrightarrow{b}$=$\overrightarrow{0}$ | B. | λ=μ=0 | C. | λ=0,$\overrightarrow{b}$=$\overrightarrow{0}$ | D. | $\overrightarrow{a}$=$\overrightarrow{0}$,μ=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com