
分析 由题意画出图形,利用平面向量的坐标运算得答案.
解答 解:由题意作图如下,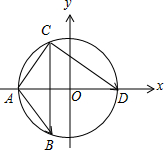
则A(-1,0),B(-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$),C(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),D(1,0).
∴$\overrightarrow{AB}•\overrightarrow{CD}=(\frac{1}{2},-\frac{\sqrt{3}}{2})•(\frac{3}{2},-\frac{\sqrt{3}}{2})$=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查平面向量的数量积运算,考查了数形结合的解题思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 18 | C. | 20 | D. | 22 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $-\frac{1}{4}$ | C. | $\frac{{\sqrt{15}}}{4}$ | D. | $-\frac{{\sqrt{15}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{π}{3}}]$ | B. | $({0,\frac{π}{3}})$ | C. | $({0,\frac{π}{6}}]$ | D. | $({0,\frac{π}{6}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ln2 | B. | ln2+1 | C. | 1 | D. | $\frac{{{e^2}-1}}{{4{e^2}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
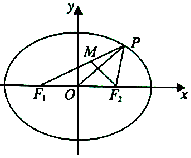 如图所示,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,其中a>b>0,F1,F2分别为其左,右焦点,点P是椭圆C上一点,PO⊥F2M,且$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$.
如图所示,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,其中a>b>0,F1,F2分别为其左,右焦点,点P是椭圆C上一点,PO⊥F2M,且$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com