
| A. | $\overrightarrow{a}$=$\overrightarrow{0}$,$\overrightarrow{b}$=$\overrightarrow{0}$ | B. | λ=μ=0 | C. | λ=0,$\overrightarrow{b}$=$\overrightarrow{0}$ | D. | $\overrightarrow{a}$=$\overrightarrow{0}$,μ=0 |
分析 $\overrightarrow{a}$,$\overrightarrow{b}$不共线,从而可以由平面向量基本定理得到λ=μ=0,即A正确.
解答 解:根据平面向量基本定理,由λ$\overrightarrow{a}$+μ$\overrightarrow{b}$=$\overrightarrow{0}$,
得:λ=μ=0.
故选:B.
点评 考查平面向量基本定理:$\overrightarrow{c}$=λ$\overrightarrow{a}$+μ$\overrightarrow{b}$,其中需$\overrightarrow{a}$,$\overrightarrow{b}$不共线,知道$\overrightarrow{0}$=0•$\overrightarrow{a}$+0•$\overrightarrow{b}$是解题的关键,本题是一道基础题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:解答题
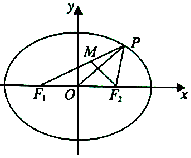 如图所示,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,其中a>b>0,F1,F2分别为其左,右焦点,点P是椭圆C上一点,PO⊥F2M,且$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$.
如图所示,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,其中a>b>0,F1,F2分别为其左,右焦点,点P是椭圆C上一点,PO⊥F2M,且$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p∧¬q | B. | ¬p∧q | C. | p∧¬q | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com