
分析 (1)由f(x)在R上为奇函数便可得到f(0)=0,从而可以求出a=1;
(2)分离常数得到$f(x)=1-\frac{2}{1+{2}^{x}}$,可看出f(x)在R上单调递增,根据增函数的定义,设任意的x1,x2∈R,且x1<x2,然后作差,通分,根据指数函数的单调性证明f(x1)<f(x2)便可得出f(x)在R上单调递增;
(3)可设g(x)=x2-2x-a,可看出g(x)的对称轴为x=1,从而有g(1)≤g(x)<g(0),或g(1)≤g(x)<g(3),这样根据f(x)在R上单调递增便有f[g(1)]≤f[g(x)]<f[g(0)],或f[g(1)]≤f[g(x)]<f[g(3)],而要使方程f(x2-2x-a)=0在(0,3)上恒有解,则需$\left\{\begin{array}{l}{f[g(1)]≤0}\\{f[g(0)]>0,或f[g(3)]>0}\end{array}\right.$,这样即可求出实数a的取值范围.
解答 解:(1)f(x)为R上的奇函数;
∴f(0)=$\frac{a-1}{1+1}=0$;
∴a=1;
(2)$f(x)=\frac{{2}^{x}-1}{1+{2}^{x}}$=$\frac{1+{2}^{x}-2}{1+{2}^{x}}=1-\frac{2}{1+{2}^{x}}$,f(x)在R上单调递增,证明如下:
设x1,x2∈R,且x1<x2,则:
$f({x}_{1})-f({x}_{2})=\frac{2}{1+{2}^{{x}_{2}}}-\frac{2}{1+{2}^{{x}_{1}}}$=$\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{(1+{2}^{{x}_{2}})(1+{2}^{{x}_{1}})}$;
∵x1<x2;
∴${2}^{{x}_{1}}<{2}^{{x}_{2}}$,${2}^{{x}_{1}}-{2}^{{x}_{2}}<0$;
又$(1+{2}^{{x}_{2}})(1+{2}^{{x}_{1}})>0$;
∴f(x1)<f(x2);
∴f(x)在R上单调递增;
(3)设g(x)=x2-2x-a,g(x)的对称轴为x=1,则:g(1)≤g(x)<g(0),或g(1)≤g(x)<g(3);
f(x)在R上单调递增;
∴f[g(1)]≤f[g(x)]<f[g(0)],或f[g(1)]≤f[g(x)]<f[g(3)];
∵方程f(x2-2x-a)=0在(0,3)上恒有解;
∴$\left\{\begin{array}{l}{f[g(1)]≤0}\\{f[g(0)]>0,或f[g(3)]>0}\end{array}\right.$;
∴$\left\{\begin{array}{l}{1-\frac{2}{1+{2}^{-1-a}}≤0}\\{1-\frac{2}{1+{2}^{-a}}>0,或1-\frac{2}{1+{2}^{3-a}}>0}\end{array}\right.$;
解得-1≤a<3;
∴实数a的取值范围为[-1,3).
点评 考查奇函数的定义,奇函数在原点有定义时,在原点处的函数值为0,分离常数法的运用,增函数的定义,以及根据增函数的定义判断并证明一个函数为增函数的方法和过程,二次函数的对称轴,二次函数的最值,清楚方程的解和函数的零点的关系,要熟悉二次函数的图象.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:选择题
| A. | a>b | B. | $\root{3}{a}>\root{3}{b}$ | C. | $\root{3}{a}=\root{3}{b}$且$\root{3}{a}>\root{3}{b}$ | D. | $\root{3}{a}=\root{3}{b}$或$\root{3}{a}>\root{3}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:解答题
选修4-5:不等式选讲
已知函数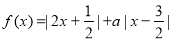 .
.
(1)当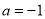 时,解不等式
时,解不等式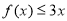 ;
;
(2)当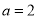 时,若关于
时,若关于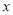 的不等式
的不等式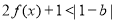 的解集为空集,求实数
的解集为空集,求实数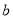 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
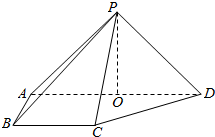 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是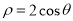 ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是
,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于两点A,B,且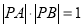 ,求实数m的值.
,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com