
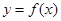 在区间
在区间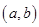 的导函数为
的导函数为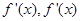 在区间
在区间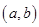 的导函数为
的导函数为 若在区间
若在区间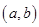 上
上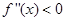 恒成立,则称函数
恒成立,则称函数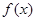 在区间
在区间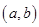 上为“凸函数”,已知
上为“凸函数”,已知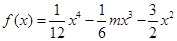 ,若对任意的实数m满足
,若对任意的实数m满足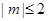 时,函数
时,函数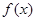 在区间
在区间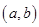 上为“凸函数”,则
上为“凸函数”,则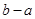 的最大值为( )
的最大值为( )| A.4 | B.3 | C.2 | D.1 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
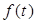 (元)与时间
(元)与时间 (天)的函数关系近似满足
(天)的函数关系近似满足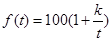 (
(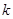 为正的常数),日销售量
为正的常数),日销售量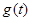 (件)与时间
(件)与时间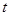 (天)的函数关系近似满足
(天)的函数关系近似满足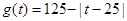 ,且第25天的销售金额为13000元.
,且第25天的销售金额为13000元.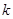 的值;
的值;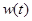 关于时间
关于时间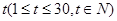 的函数关系式,并求前半个月销售金额
的函数关系式,并求前半个月销售金额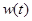 的最小值。
的最小值。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
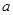 吨,计划正式运营后的第一年进油量为已储油量的
吨,计划正式运营后的第一年进油量为已储油量的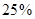 ,以后每年的进油量为上一年年底储油量的
,以后每年的进油量为上一年年底储油量的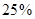 ,且每年运出
,且每年运出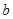 吨,设
吨,设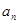 为正式运营第n年年底的储油量。(其中
为正式运营第n年年底的储油量。(其中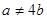 )
)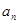 的表达式
的表达式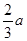 吨,如果
吨,如果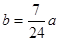 吨,该油库能否长期按计划运营?如果可以请加以证明;如果不行请求出最多可以运营几年。(取
吨,该油库能否长期按计划运营?如果可以请加以证明;如果不行请求出最多可以运营几年。(取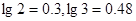 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
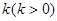 .现已知相距
.现已知相距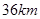 的
的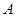 ,
,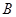 两家化工厂(污染源)的污染强度分别为正数
两家化工厂(污染源)的污染强度分别为正数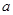 ,
,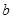 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数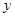 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设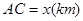 .
.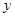 表示为
表示为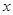 的函数;
的函数; 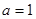 时,
时,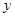 在
在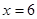 处取得最小值,试求
处取得最小值,试求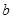 的值.
的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com