
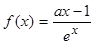 .
.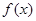 的单调区间;
的单调区间;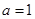 时,若方程
时,若方程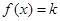 有两个不同的实根
有两个不同的实根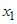 和
和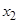 ,
,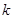 的取值范围;
的取值范围;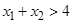 .
.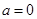 时,
时,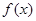 在
在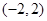 递增;
递增; 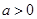 时,
时,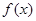 在
在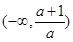 递增;
递增; 递减
递减 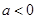 时,
时,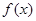 在
在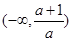 递减;
递减; 递增
递增 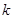 的取值范围是
的取值范围是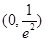 (ⅱ)
(ⅱ)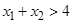
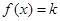 有两个不同的实根,则可以分析函数y=f(x)的图像的变化情况,确定参数k的取值范围。同时借助于单调性证明不等式
有两个不同的实根,则可以分析函数y=f(x)的图像的变化情况,确定参数k的取值范围。同时借助于单调性证明不等式
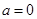 时,
时,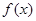 在
在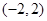 递增; 又
递增; 又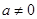 时
时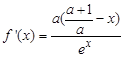
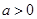 时,
时,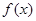 在
在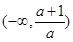 递增;
递增; 递减
递减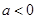 时,
时,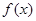 在
在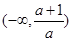 递减;
递减; 递增 5分
递增 5分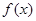 在
在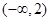 递增;
递增;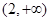 递减 ∴
递减 ∴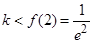 6分
6分 ,而
,而 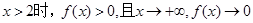 ∴
∴
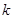 的取值范围是
的取值范围是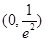 8分
8分 ,则
,则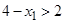
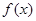 在
在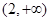 递减,∴要证
递减,∴要证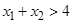 . 即证
. 即证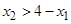 .
. 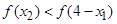 ,即证
,即证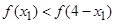
 ,
,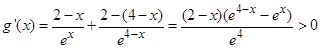
 在
在 递增 ∴
递增 ∴ ,即
,即 ,即
,即 , ∴
, ∴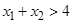


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源:不详 题型:解答题
 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com