
| A. | $\frac{5\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{3\sqrt{3}}{2}$ |
分析 由$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$得到P为重心,由$\overrightarrow{PA}$•$\overrightarrow{PB}$=$\overrightarrow{PB}$•$\overrightarrow{PC}$=$\overrightarrow{PC}$•$\overrightarrow{PA}$,得到P又为垂心,得到三角形为等边三角形,根据$\overrightarrow{PA}$•$\overrightarrow{PB}$=-1以及向量的数量积公式和解直角三角形得到边长为$\sqrt{6}$,即可求出三角形的面积.
解答 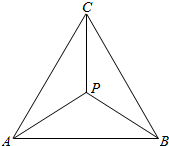 解:∵$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$,则$\overrightarrow{PA}$+$\overrightarrow{PB}$=-$\overrightarrow{PC}$,
解:∵$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$,则$\overrightarrow{PA}$+$\overrightarrow{PB}$=-$\overrightarrow{PC}$,
由平行四边形法则,得CP延长交AB于中点,
同理,BP延长交AC于中点,∴P为重心;
∵$\overrightarrow{PA}$•$\overrightarrow{PB}$=$\overrightarrow{PB}$•$\overrightarrow{PC}$=$\overrightarrow{PC}$•$\overrightarrow{PA}$,∴$\overrightarrow{PB}$($\overrightarrow{PA}$-$\overrightarrow{PC}$)=0,
即PB⊥AC,同理PC⊥AB,∴P又为垂心,
∴三角形ABC为等边三角形,
∵$\overrightarrow{PA}$•$\overrightarrow{PB}$=-1,
∴|$\overrightarrow{PA}$|•|$\overrightarrow{PB}$|cos120°=-1,
∴|$\overrightarrow{PA}$|=|$\overrightarrow{PB}$|=$\sqrt{2}$,
∴|AB|=2|AP|cos30°=$\sqrt{6}$
∴S△ABC=$\frac{\sqrt{3}}{4}$×($\sqrt{6}$)2=$\frac{3\sqrt{3}}{2}$,
故选:D.
点评 本题考查两向量的数量积的运算,以及两向量的和、垂直的条件,考查三角形的重心和垂心,考查基本的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABC-A1B1C1中,D是AB的中点,且AA1=AC=3,BC1=AB=5.
如图,在直三棱柱ABC-A1B1C1中,D是AB的中点,且AA1=AC=3,BC1=AB=5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x${\;}^{\frac{1}{2}}$ | B. | f(x)=(-x)${\;}^{\frac{1}{2}}$ | C. | f(x)=-(-x)${\;}^{\frac{1}{2}}$ | D. | f(x)=-x${\;}^{\frac{1}{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{2π}{3}$个单位 | B. | 向右平移$\frac{2π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -sinx | C. | cosx | D. | sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-4)∪(\frac{2}{3},+∞)$ | B. | $(-∞,-2)∪(\frac{2}{3},+∞)$ | C. | $(-2,\frac{2}{3})$ | D. | $(-4,\frac{2}{3})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com