
���� �������о���������ż�ԣ�Ȼ������������ͼ�ݴ���⣮
��� �⣺����f��x��=$\frac{4}{|x|+2}$-1��֪�����Ķ�����ΪR����f��-x��=f��x�����ʺ���Ϊż�������ʢ���ȷ��
��x��0ʱ������f��x��=$\frac{4}{|x|+2}$-1=$\frac{4}{x+2}-1$���ú����ڣ�0��+�ޣ��ϼ���������x=0ʱ��f��x��=1����x��+��ʱ��f��x����-1��������ֵ��Ϊ����-1��1]�����Ԣ���ȷ��
�����ż�ԣ�����f��x����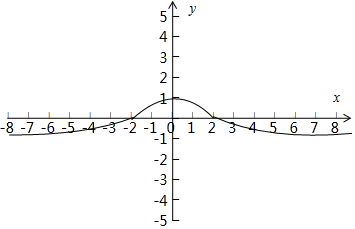 ͼ�����£�
ͼ�����£�
��֪������ֵ���ǣ�-1��1�����ʢ���ȷ��
����y=f��x����g��x��=2x-2����Ϻ�����ͼ��֪x=0ʱ��g��0��=$\frac{1}{4}$������һ�������㲻��ȷ�����Ԣ۲���ȷ��
��f��x��=$\frac{4}{|x|+2}$-1������[a��b]��a��bΪ�������ϵ�ֵ����[0��1]���������������������ԣ�a��b������5�ԣ��ֱ�Ϊ��-2��0������-2��1������-2��2������-1��2������0��2�����Ԣ���ȷ��
����ȷ�������Ǣ٢ڢܣ�
�ʴ�Ϊ���٢ڢܣ�
���� ���⿼���˺��������ʣ�һ�����о�������Ȼ���жϺ�������ż�ԡ������Ե�������Ϊͻ�ƿڣ���һЩҪ��Ϻ�����ͼ����Է�����ע�����ν�ϵ�˼���Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��x��=x0��f��x��=1 | B�� | f��x��=$\sqrt{{x}^{2}}$-1��f��x��=|x|-1 | ||
| C�� | f��x��=$\frac{{x}^{2}-4}{x+2}$��f��x��=x-2 | D�� | f��x��=$\sqrt{��x-1����x-2��}$��f��x��=$\sqrt{x-1}$$\sqrt{x-2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=log2x | B�� | y=$\frac{1}{x^2}$ | C�� | y=$\frac{1}{2^x}$ | D�� | y=$\frac{1}{{\sqrt{x}}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com