练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    己知sinθ+cosθ=
    1
    4
    ，则sin2θ等于（　　）
    A、-
    		15
    4
    B、
    		15
    4
    C、-
    15
    16
    D、
    15
    16
    考点：二倍角的正弦
    专题：计算题,三角函数的求值
    分析：两边平方，然后逆用二倍角公式即可求出sin2θ的值．
    解答： 解：∵sinθ+cosθ=
    1
    4
    ，
    ∴1+2sinθcosθ=
    1
    16

    ∴sin2θ=-
    15
    16

    故选C．
    点评：本题主要考查了二倍角的正弦公式的逆用，解题时要注间分析角的关系，条件中是单角，求的是倍角，通过平方逆用二倍公式可以转化．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知x∈（
    1
    2
    ，1），a=log2x，b=2a，c=2a，则（　　）
    A、a＜b＜c
    B、c＜a＜b
    C、b＜a＜c
    D、b＜c＜a

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    “单独二胎”政策的落实是我国完善计划生育基本国策的一项重要措施，事先需要做大量的调研论证．现为了解我市市民对该项措施是否认同，拟从全体市民中抽取部分样本进行调查．调查结果如下表：
    调查人数 2 10 70 130 310 700 1500 2000 3000 5000
    认同人数 2 9 60 116 286 639 1339 1810 2097 4515
    认同频率 1 0.9 0.857 0.892 0.922 0.913 0.893 0.905 0.899 0.903
    则根据上表我们可以推断市民认同该项措施的概率最有可能为（　　）
    A、0.80B、0.85
    C、0.90D、0.92

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知{an}是等比数列，a1=-1，a4=64，则S4=（　　）
    A、-51B、64C、85D、51

    查看答案和解析>>

    科目：高中数学 来源： 题型：

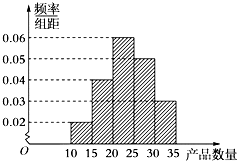    为了调查某厂2000名工人生产某种产品的能力，随机抽查了20位工人某天生产该产品的数量，产品数量的分组区间为[10，15），[15，20），[20，25），[25，30），[30，35]，频率分布直方图如图所示．工厂规定从生产低于20件产品的工人中随机地选取2位工人进行培训，则这2位工人不在同一组的概率是（　　）
    A、
    1
    10
    B、
    7
    15
    C、
    8
    15
    D、
    13
    15

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知长方体ABCD-A1B1C1D1，其中AB=BC=2，过A1、C1、B三点的平面截去长方体的一个角后．得到如图所示的几何体，且这个几何体的体积为
    40
    3
    ．
    （1）求几何体ABCD-A1C1D1的表面积；
    （2）在线段BC1上是否存在点P，使直线A1P与C1D垂直，如果存在，求线段A1P的长，如果不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    △ABC中，a，b，c分别是角A，B，C的对边，
    m
    =（2a+c，b），
    n
    =（cosB，cosC），且
    m
    •
    n
    =0．
    （1）求角B的大小；
    （2）若a=2，S△ABC=4
    		3
    ，求b．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知实数x、y满足y=-2x+8，且2≤x≤3，求
    y
    x
    的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设a＞0，两个函数f（x）=eax，g（x）=blnx的图象关于直线y=x对称．
    （1）求实数a，b满足的关系式；
    （2）当a取何值时，函数h（x）=f（x）-g（x）有且只有一个零点；
    （3）当a=1时，在（
    1
    2
    ，+∞）上解不等式f（1-x）+g（x）＜x2．

    查看答案和解析>>

    同步练习册答案