
分析 (Ⅰ)由${a_1}=a+\frac{1}{a}>2$,可求得an>2,${a_{n+1}}-{a_n}={a_n}^2-{a_n}-2=({a_n}-2)({a_n}+1)>0$,即可证明an+1>an;
(Ⅱ)由递推式分别求得a1,a2,a3…an,采用裂项法分别求得:$\frac{1}{{a}_{1}}$,$\frac{1}{{a}_{1}{a}_{2}}$,…$\frac{1}{{a}_{1}{a}_{2}{a}_{3}…{a}_{n}}$,则$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{1}{a}_{2}}$+…+$\frac{1}{{a}_{1}{a}_{2}{a}_{3}…{a}_{n}}$=a,由题意求得实数a的取值范围.
解答 解:(Ⅰ)证明:∵${a_1}=a+\frac{1}{a}>2$,
且${a_{n+1}}-2={a_n}^2-4=({a_n}-2)({a_n}+2)$,
∴an>2
又${a_{n+1}}-{a_n}={a_n}^2-{a_n}-2=({a_n}-2)({a_n}+1)>0$,
∴an+1>an…(5分)
(Ⅱ)∵${a_1}=a+\frac{1}{a}=\frac{{{a^2}+1}}{a}$,
∴${a_2}={a_1}^2-2={a^2}+\frac{1}{a^2}=\frac{{{a^4}+1}}{a^2}$,
${a_3}={a_2}^2-2={a^4}+\frac{1}{a^4}=\frac{{{a^8}+1}}{a^4}$,
…
${a_n}={a_{n-1}}^2-2=\frac{{{a^{2^n}}+1}}{{{a^{{2^{n-1}}}}}}$,
∴$\frac{1}{a_1}=\frac{1}{a}(1-\frac{1}{{{a^2}+1}})$,
∴$\frac{1}{{{a_1}{a_2}}}=\frac{a}{{{a^2}+1}}•\frac{a^2}{{{a^4}+1}}=\frac{1}{a}[\frac{1}{{{a^2}+1}}-\frac{1}{{({a^2}+1)({a^4}+1)}}]$,
…
$\frac{1}{{{a_1}{a_2}{a_3}…{a_n}}}=\frac{1}{a}[\frac{1}{{({a^2}+1)({a^4}+1)…({a^{{2^{n-1}}}}+1)}}-\frac{1}{{({a^2}+1)({a^4}+1)…({a^{2^n}}+1)}}]$,
∴$\frac{1}{a_1}+\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_1}{a_2}{a_3}}}+…+\frac{1}{{{a_1}{a_2}{a_3}…{a_n}}}$,
=$\frac{1}{a}[1-\frac{1}{{({a^2}+1)({a^4}+1)…({a^{2^n}}+1)}}]$,
=$\frac{1}{a}(1-\frac{{1-{a^2}}}{{1-{a^{{2^{n+1}}}}}})<\frac{1}{a}[1-(1-{a^2})]=a$,
由题意$a≤\frac{1}{2}$,
所以$0<a≤\frac{1}{2}$.…(15分)
点评 本题考查数列的递推公式,根据数列前几项,归纳出数列的通项公式,采用”裂项法“求数列的前n项和,考查观察及归纳推理能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{100}{3}$π | B. | $\frac{200}{3}$π | C. | $\frac{400}{3}$π | D. | $\frac{400}{9}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
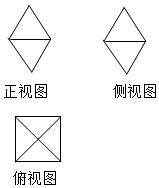 一个几何体的三视图如图所示(单位:m),其正视图、侧视图均有一个角为60°的菱形,俯视图为边长为1的正方形,则该几何体的体积为$\frac{\sqrt{3}}{3}$m3.
一个几何体的三视图如图所示(单位:m),其正视图、侧视图均有一个角为60°的菱形,俯视图为边长为1的正方形,则该几何体的体积为$\frac{\sqrt{3}}{3}$m3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com