
分析 根据向量的坐标运算法则计算即可.
解答 解:(1)$\overrightarrow a$=(2,1),$\overrightarrow b$=(-3,4),
∴$\overrightarrow a$+$\overrightarrow b$=(-1,5),$\overrightarrow a$-$\overrightarrow b$=(5,-3),3$\overrightarrow a$+4$\overrightarrow b$=(-6,19)
(2)∵$\overrightarrow a+\overrightarrow b=({2,-8})$,$\overrightarrow a-\overrightarrow b=({-8,16})$,
∴2$\overrightarrow a$=($\overrightarrow a$+$\overrightarrow b$)+($\overrightarrow a$-$\overrightarrow b$)=(-6,8),
∴$\overrightarrow a$=(-3,4),
∴2$\overrightarrow{b}$=($\overrightarrow a$+$\overrightarrow b$)-($\overrightarrow a$-$\overrightarrow b$)=(10,-24),
∴$\overrightarrow b$=(5,-12)
点评 本题考查了向量的坐标运算,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 12 | D. | 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7\sqrt{2}}{2}$ | B. | $\sqrt{29}$ | C. | 5 | D. | 以上都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
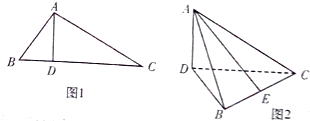 如图1,在Rt△ABC中,∠ABC=60°,∠BAC=90°,AD是BC上的高,沿AD将△ABC折成600的二面角B-AD-C,如图2.
如图1,在Rt△ABC中,∠ABC=60°,∠BAC=90°,AD是BC上的高,沿AD将△ABC折成600的二面角B-AD-C,如图2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=x+\frac{4}{x}≥2\sqrt{x•\frac{4}{x}}=4$ | |
| B. | $y=sinx+\frac{4}{sinx}≥2\sqrt{sinx•\frac{4}{sinx}}=4\;(x为锐角)$ | |
| C. | $y=lgx+4{log_x}10≥2\sqrt{lgx•4{{log}_x}10}=4$ | |
| D. | $y={3^x}+\frac{4}{3^x}≥2\sqrt{{3^x}•\frac{4}{3^x}}=4$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com