考点:与二面角有关的立体几何综合题,异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:(1)连接A1B,记A1B与AB1的交点为F,作CG⊥AB,G为垂足,连接DG,由此利用三垂线定理,能证明DE⊥CD.
(2)由DG∥AB1,知∠CDG为异面直线AB1与CD的夹角或其补角,由此能求出异面直线AB1与CD的夹角的大小.
解答:
(1)证明:连接
A1B,记
A1B与
AB1的交点为
F.
作
CG⊥
AB,
G为垂足,
因为面
AA1BB1为正方形,故
A1B⊥
AB1,且
AF=
FB1,
又
AE=3
EB1,所以
FE=
EB1,
又
D为
BB1的中点,故
DE∥
BF,
DE⊥
AB1.
由
AC=
BC知,
G为
AB中点.
又由底面
ABC⊥面
AA1B1B.

连接
DG,则
DG∥
AB1,故
DE⊥
DG,
由三垂线定理,得
DE⊥
CD.
(2)解:由(1)知因为
DG∥
AB1,
故∠
CDG为异面直线
AB1与
CD的夹角或其补角.
因为
AB=2,则
AB1=2
,
DG=
.作
B1H⊥
A1C1,
H为垂足,
因为底面
A1B1C1⊥面
AA1CC1,故
B1H⊥面
AA1C1C.
又作
HK⊥
AC1,
K为垂足,
连接
B1K,由三垂线定理,得
B1K⊥
AC1,
因此∠
B1KH为二面角A
1-AC
1-B
1的平面角.
由tan
∠B1KH==
,
取
A1B1的中点
G1,连结
C1G1,
设
CG=
x,则
C1G1=
CG=
x,
A1C1=,C
1G
1•A
1B
1=A
1C
1•B
1H,
∴
B1H==
,
∴HK=
=
,
C1H==
,
又△
C1HK∽△
C1AA1,∴
=,
=,
∴13x
4-33x
2+14=0,解得x=
,或x=
(舍)
∴CG=
,tan∠CGD=1,∴∠
CDG=45°,
∴异面直线AB
1与CD的夹角的大小为45°.
点评:本题考查异面直线垂直的证明,考查异面直线AB1与CD的夹角的大小的求法,解题时要认真审题,注意空间思维能力的培养.

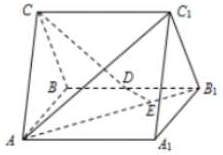 如图,直三棱柱ABC-A1B1C1中,AC=BC,C到AB的距离大于1,AA1=AB=2,D为BB1的中点,E为AB1上的一点,AE=3EB1.
如图,直三棱柱ABC-A1B1C1中,AC=BC,C到AB的距离大于1,AA1=AB=2,D为BB1的中点,E为AB1上的一点,AE=3EB1.

