
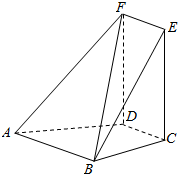
 如图,在多面体EF-ABCD中,ABCD,ABEF均为直角梯形,∠ABE=∠ABC=$\frac{π}{2}$,DCEF为平行四边形,平面DCEF⊥平面ABCD.
如图,在多面体EF-ABCD中,ABCD,ABEF均为直角梯形,∠ABE=∠ABC=$\frac{π}{2}$,DCEF为平行四边形,平面DCEF⊥平面ABCD.分析 (1)由∠ABE=∠ABC=$\frac{π}{2}$可得AB⊥平面BCE,于是EF⊥平面BCE,从而EF⊥CE,故四边形CDFE为矩形,于是D⊥CD,根据面面垂直的性质得出DF⊥平面ABCD;
(2)连接BD,DE,则∠FBD为BF与平面ABCD所成角,故而得出DF=BD=2,计算出BC,CD,根据VB-DEF=VE-BDF列方程即可得出点E到平面BDF的距离.
解答 证明:(1)∵$∠ABE=∠ABC=\frac{π}{2}$,
∴AB⊥BE,AB⊥BC,又BE?平面BCE,BC?平面BCE,BE∩BC=B,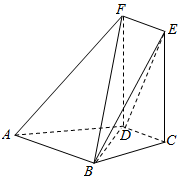
∴AB⊥平面BCE,∵EF∥AB,
∴EF⊥平面BCE,∵CE?平面BCE,
∴EF⊥CE.又四边形CDFE是平行四边形,
∴四边形CDFE是矩形,
∴DF⊥DC.
又平面DCEF⊥平面ABCD,且平面ABCD∩平面CDFE=CD,DF?平面CDFE,
∴DF⊥平面ABCD.
(2)连接BD,DE.
∵△ABD是边长为2的等边三角形,四边形ABCD是直角梯形,∠ABC=$\frac{π}{2}$,
∴$BD=2,CD=1,BC=\sqrt{3}$.
由(1)得DF⊥平面ABCD,∴∠FBD为BF与平面ABCD所成角的角,
∴tan∠FBD=1,即DF=BD=2.
∴VB-DEF=$\frac{1}{3}{S}_{△DEF}•BC$=$\frac{1}{3}×\frac{1}{2}×1×2×\sqrt{3}$=$\frac{\sqrt{3}}{3}$.
设E到平面BDF的距离为d,则VE-BDF=$\frac{1}{3}{S}_{△BDF}•d$=$\frac{1}{3}×\frac{1}{2}×2×2×d$=$\frac{2d}{3}$
∵VB-DEF=VE-BDF,∴$\frac{2d}{3}$=$\frac{\sqrt{3}}{3}$,解得$d=\frac{{\sqrt{3}}}{2}$.
点评 本题考查了线面垂直的判定,空间距离的计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{32π}{3}$ | B. | $\frac{32\sqrt{3}π}{3}$ | C. | $\frac{64π}{3}$ | D. | $\frac{64\sqrt{2}π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 对教师管理水平好评 | 对教师管理水平不满意 | 合计 | |
| 对教师教学水平好评 | |||
| 对教师教学水平不满意 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
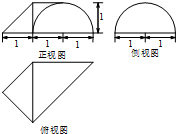
| A. | $\frac{π}{3}$ | B. | $\frac{5π}{6}$ | C. | $\frac{2π}{3}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{asinαsinβ}{sin(α-β)}$ | B. | $\frac{asinαsinβ}{cos(α-β)}$ | C. | $\frac{acosαcosβ}{sin(α-β)}$ | D. | $\frac{acosαcosβ}{cos(α-β)}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{7}$ | B. | 3 | C. | $\sqrt{11}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=3x3+2x2+1 | B. | f(x)=${x^{-\frac{1}{2}}}$ | C. | f(x)=3x | D. | f(x)=$\frac{{\sqrt{4-{x^2}}}}{{|{x+3}|-3}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com