
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{3}{2}$ |
分析 由题意分两种情况求解,分别求出双曲线的渐近线方程,再求出平移后的直线方程,与抛物线方程联立化简后,由相切的条件可得△=0,化简后由a、b、c的关系求出离心率.
解答 解:(1)当双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线方程为:$y=-\frac{b}{a}x$,
此渐近线向上平移两个单位可得,$y=-\frac{b}{a}x+2$,
则由$\left\{\begin{array}{l}{y=-\frac{b}{a}x+2}\\{{y}^{2}=4x}\end{array}\right.$得,$\frac{{b}^{2}}{{a}^{2}}{x}^{2}-(\frac{4b}{a}+4)x+4=0$,
所以△=$(\frac{4b}{a}+4)^{2}-4×\frac{{b}^{2}}{{a}^{2}}×4=0$,
化简得,$\frac{2b}{a}+1=0$,不成立;
(2)当双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线方程为:$y=\frac{b}{a}x$,
此渐近线向上平移两个单位可得,$y=\frac{b}{a}x+2$,
则由$\left\{\begin{array}{l}{y=\frac{b}{a}x+2}\\{{y}^{2}=4x}\end{array}\right.$得,$\frac{{b}^{2}}{{a}^{2}}{x}^{2}+(\frac{4b}{a}-4)x+4=0$,
所以△=${(\frac{4b}{a}-4)}^{2}-4×\frac{{b}^{2}}{{a}^{2}}×4=0$,
化简得,$-\frac{2b}{a}+1=0$,则a=2b,
所以c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{5}b$,即e=$\frac{c}{a}$=$\frac{\sqrt{5}}{2}$,
故选:A.
点评 本题考查求双曲线离心率、标准方程与简单几何性质,直线与抛物线的位置关系,考查了化简、变形能力.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 0<k≤12 | B. | 0<k<12 | C. | 0<k≤12或k=8$\sqrt{3}$ | D. | 0<k<12或k=8$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\sqrt{x}$ | B. | y=-sinx | C. | $y=\frac{1}{x}$ | D. | $y=\frac{{{x^2}-1}}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
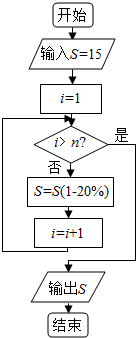 某人以15万元买了一辆汽车,此汽车将以每年20%的速度折旧,如图是描述汽车价值变化的算法流程图,则当n=4吋,最后输出的S的值为( )
某人以15万元买了一辆汽车,此汽车将以每年20%的速度折旧,如图是描述汽车价值变化的算法流程图,则当n=4吋,最后输出的S的值为( )| A. | 9.6 | B. | 7.68 | C. | 6.144 | D. | 4.9152 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com