
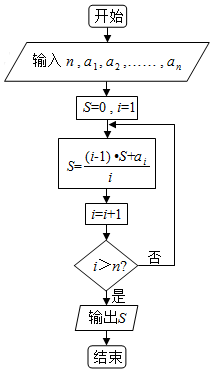
 执行如图所示的程序框图,若输入数据n=5,a1=-2,a2=-2.6,a3=3.2,a4=2.5,a5=1.4,则输出的结果为0.5.
执行如图所示的程序框图,若输入数据n=5,a1=-2,a2=-2.6,a3=3.2,a4=2.5,a5=1.4,则输出的结果为0.5. 分析 根据输入的n的值和5个数据,判断循环变量和5的大小,当i>5不成立时进入循环体依次对S替换,i>5成立时结束算法,从而得解.
解答 解:模拟执行程序,可得
赋值S=0,i=1,执行S=$\frac{(i-1)•S+{a}_{1}}{i}$=$\frac{(1-1)×0+(-2)}{1}$=-2,i=1+1=2;
判断2>5,执行S=$\frac{(i-1)•S+{a}_{2}}{i}$=$\frac{(2-1)×(-2)+(-2.6)}{2}$=-2.3,i=2+1=3;
判断3>5,执行S=$\frac{(i-1)•S+{a}_{3}}{i}$=$\frac{(3-1)×(-2.3)+3.2}{3}$=-$\frac{7}{15}$,i=3+1=4;
判断4>5,执行S=$\frac{(i-1)•S+{a}_{4}}{i}$=$\frac{(4-1)×(-\frac{7}{15}+2.5)}{4}$=0.275,i=4+1=5;
判断5>5,执行S=$\frac{(i-1)•S+{a}_{5}}{i}$=$\frac{(5-1)×0.275+1.4}{5}$=0.5,i=5+1=6;
判断6>5,算法结束,输出的结果为0.5.
故答案为:0.5.
点评 本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结果,属于基础题.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:解答题
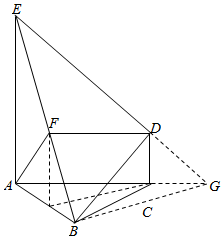 如图所示,△ABC是正三角形,线段EA和DC都垂直于平面ABC,设EA=AB=2a,且F为的BE中点
如图所示,△ABC是正三角形,线段EA和DC都垂直于平面ABC,设EA=AB=2a,且F为的BE中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | $-\frac{2}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
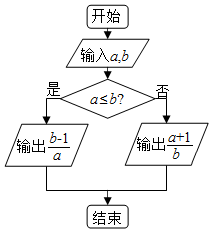 若对任意非零实数a,b,若a*b的运算规则如图的程序框图所示,则(3*2)*4的值是( )
若对任意非零实数a,b,若a*b的运算规则如图的程序框图所示,则(3*2)*4的值是( )| A. | $\frac{13}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
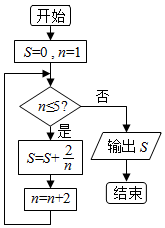
| A. | $\frac{8}{3}$ | B. | $\frac{46}{15}$ | C. | $\frac{25}{6}$ | D. | $\frac{137}{30}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com