
分析 (1)学生A抛掷一次所得分数X的可能取值为1,2,3,分别求出相应的概率,由此能求出学生A抛掷一次所得分数的期望.
(2)|x-y|≥1的对立事件是x=y,由此能求出|x-y|≥1的概率.
解答 解:(1)抛掷一骰子,若掷出1点、2点、3点,则得1分,
若掷出4点、5点,则得2分,若掷出6点,则得3分,
学生A抛掷一次所得分数X的可能取值为1,2,3,
P(X=1)=$\frac{3}{6}=\frac{1}{2}$,
P(X=2)=$\frac{2}{6}=\frac{1}{3}$,
P(X=3)=$\frac{1}{6}$,
∴学生A抛掷一次所得分数的期望E(X)=$1×\frac{1}{2}+2×\frac{1}{3}+3×\frac{1}{6}$=$\frac{5}{3}$.
(2)∵学生A与学生B各掷2次,所得分数分别x,y,
∴|x-y|≥1的对立事件是x=y,
∴|x-y|≥1的概率P=1-P(x=y)=1-[$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}$+${C}_{2}^{1}(\frac{1}{2})(\frac{1}{3}){C}_{2}^{1}(\frac{1}{2})(\frac{1}{3})$+($\frac{1}{3}×\frac{1}{3}+{C}_{2}^{1}×\frac{1}{2}×\frac{1}{6}$)($\frac{1}{3}×\frac{1}{3}+{C}_{2}^{1}×\frac{1}{2}×\frac{1}{6}$)+${C}_{2}^{1}×\frac{1}{3}×\frac{1}{6}×{C}_{2}^{1}×\frac{1}{3}×\frac{1}{6}$+$\frac{1}{6}×\frac{1}{6}×\frac{1}{6}×\frac{1}{6}$]=$\frac{53}{72}$.
点评 本题考查离散型随机变量的数学期望的求法,考查概率的求法,是中档题,解题时要认真审题,注意对立事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:选择题
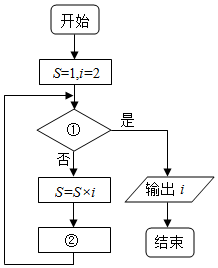
| A. | S>384,i=i+1 | B. | S≥384,i=i+2 | C. | S>3840,i=i+1 | D. | S≥3840,i=i+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
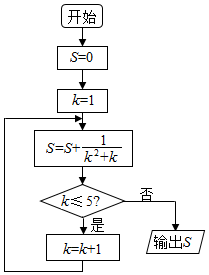
| A. | $\frac{5}{6}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com