
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
分析 利用等差中项的性质建立a,b和c的关系式,利用正弦定理把边转化成角的正弦,求得sinB的值,进而求得B.
解答 解:∵a,b,c,成等比数列,
∴b2=ac.
∵$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$,
∴sin2B=sinAsinC.
又∵sinAsinC=$\frac{3}{4}$,
∴sin2B=$\frac{3}{4}$.
∵sinB>0,
∴sinB=$\frac{\sqrt{3}}{2}$.
∴B=$\frac{π}{3}$或$\frac{2π}{3}$.
又∵a,b,c成等比数列,
∴b≤a或b≤c,即b不是△ABC的最大边,故B=$\frac{π}{3}$.
故选:B.
点评 本题主要考查了正弦定理的运用.在解三角形问题中往往通过正弦定理和余弦定理把角和边的问题互化,进而找到解决问题的突破口.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
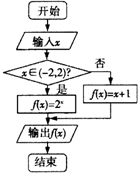
| A. | [0,log23] | B. | [-2,2] | C. | [0,log23]∪{2} | D. | [-2,log23]∪{2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 位于线段AB上 | B. | 位于线段AD上 | C. | 只能在A点 | D. | 只能在AB的中点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
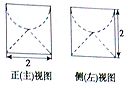 若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此时几何体的体积是( )
若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此时几何体的体积是( )| A. | 2π | B. | $\frac{4π}{3}$ | C. | π | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 50 | B. | -7 | C. | -48 | D. | -49 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-1,1) | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1]∪[1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com