
已知函数y=f(x)的图象经过坐标原点,其导函数为f ′(x)=6x-2,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)在函数y=f(x)的图象上.
(1)求数列{an}的通项公式;
(2)若数列{an}和数列{bn}满足等式:an= (n∈N*),求数列{bn}的前n项和Tn.
(n∈N*),求数列{bn}的前n项和Tn.
科目:高中数学 来源: 题型:
已知等比数列{an}的各项均为正数,公比q≠1,设P=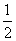 (log0.5a5+log0.5a7),Q=log0.5
(log0.5a5+log0.5a7),Q=log0.5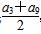 ,P与Q的大小关系是( )
,P与Q的大小关系是( )
A.P≥Q B.P<Q
C.P≤Q D.P>Q
查看答案和解析>>
科目:高中数学 来源: 题型:
某同学在电脑中打出如下若干个圈:
●○●○○●○○○●○○○○●○○○○○●……
若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前2014个圈中的●的个数是( )
A.60 B.61 C.62 D.63
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}的各项均为正数,如图给出程序框图,当k=5时,输出的S=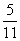 ,则数列{an}的通项公式为( )
,则数列{an}的通项公式为( )
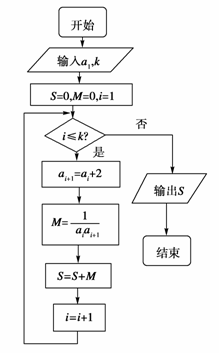
A.an=2n B.an=2n-1
C.an=2n+1 D.an=2n-3
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列四个命题:
①若a>b>0,则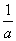 >
>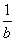 ;
;
②若a>b>0,则a-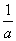 >b-
>b-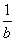 ;
;
③若a>b>0,则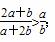
④设a,b是互不相等的正数,则|a-b|+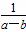 ≥2.
≥2.
其中正确命题的序号是________(把你认为正确命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
使-x2+2x≤M成立的所有常数M中,我们把M的最小值1叫做-x2+2x的“上确界”,若a,b∈R,且a+b=1,则-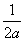 -
-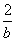 的“上确界”为( )
的“上确界”为( )
A.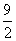 B.
B.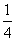 C.-
C.-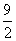 D.-4
D.-4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com