
分析 (1)根据向量平行的坐标公式即可,求sin2θ的值;
(2)根据向量垂直的坐标公式即可求cos2θ的值.
解答 解:(1)当a=0,且$\overrightarrow{m}$∥$\overrightarrow{n}$时,
则$\frac{1}{2}$(-$\frac{1}{2}$)-(-sinθ)cosθ=0,
即$-\frac{1}{4}$+sinθcosθ=0,
即sinθcosθ=$\frac{1}{4}$,
则sin2θ=$\frac{1}{8}$;
(2)当a=$\frac{\sqrt{2}}{2}$,且$\overrightarrow{m}$⊥$\overrightarrow{n}$时,
则$\overrightarrow{m}$•$\overrightarrow{n}$=0,
则($\frac{\sqrt{2}}{2}$-sinθ)×$\frac{1}{2}$-$\frac{1}{2}$cosθ=0.
即sinθ+cosθ=$\frac{\sqrt{2}}{2}$,
平方得1+sin2θ=$\frac{1}{2}$,
即sin2θ=-$\frac{1}{2}$,
则cos2θ=$±\sqrt{1-si{n}^{2}2θ}=±\frac{\sqrt{3}}{2}$.
点评 本题主要考查向量平行或向量垂直的坐标公式的计算,熟练掌握相应的坐标公式是解决本题的关键.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
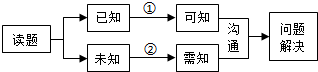 如图是解决数学问题的思维过程的流程图:图中①、②两条流程线与“推理与证明”中的思维方法相匹配是( )
如图是解决数学问题的思维过程的流程图:图中①、②两条流程线与“推理与证明”中的思维方法相匹配是( )| A. | ①-分析法,②-综合法 | B. | ①-综合法,②-分析法 | ||
| C. | ①-综合法,②-反证法 | D. | ①-分析法,②-反证法 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
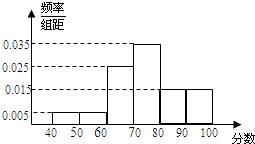 某校1000名学生的高中数学学业水平考试成绩的频率分布直方图如图所示.则不低于60分的人数是( )
某校1000名学生的高中数学学业水平考试成绩的频率分布直方图如图所示.则不低于60分的人数是( )| A. | 800 | B. | 900 | C. | 950 | D. | 990 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 不充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com