
| A. | $\frac{π}{27}$ | B. | $\frac{2π}{27}$ | C. | $\frac{π}{9}$ | D. | $\frac{2π}{9}$ |
分析 作出不等式组对应的平面区域,求出面积求出圆(x-1)2+(y-3)2=4在区域内的面积,再求概率即可.
解答 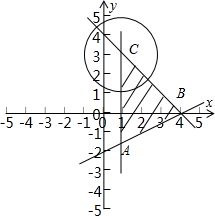 解:实数x,y满足约束条件$\left\{\begin{array}{l}x+y≤4\\ x-2y-4≤0\\ x≥1\end{array}\right.$,对应的平面区域如图所示,C(1,3),A(1,-$\frac{3}{2}$),B(4,0),其面积为$\frac{1}{2}×\frac{9}{2}×3$=$\frac{27}{4}$,
解:实数x,y满足约束条件$\left\{\begin{array}{l}x+y≤4\\ x-2y-4≤0\\ x≥1\end{array}\right.$,对应的平面区域如图所示,C(1,3),A(1,-$\frac{3}{2}$),B(4,0),其面积为$\frac{1}{2}×\frac{9}{2}×3$=$\frac{27}{4}$,
由于∠ACB=45°,所以圆(x-1)2+(y-3)2=4在区域内的面积为$\frac{1}{8}×π×4$=$\frac{π}{2}$,
所以所求的概率为$\frac{\frac{π}{2}}{\frac{27}{4}}$=$\frac{2π}{27}$,
故选:B.
点评 本题主要考查几何概型的概率的计算,确定对应的区域的面积,利用数形结合是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数y=f(x)(x∈R)是奇函数,其部分图象如图所示,则在(-2,0)上与函数
已知函数y=f(x)(x∈R)是奇函数,其部分图象如图所示,则在(-2,0)上与函数| A. | y=x2+1 | B. | y=log2|x| | ||
| C. | $y=\left\{\begin{array}{l}{e^x}(x≥0)\\{e^{-x}}(x<0)\end{array}\right.$ | D. | y=cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
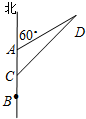 如图,机车甲、乙分别停在A,B处,且AB=10km,甲的速度为4千米/小时,乙的速度是甲的$\frac{1}{2}$,甲沿北偏东60°的方向移动,乙沿正北方向移动,若两者同时移动100分钟,则它们之间的距离为$\frac{20\sqrt{3}}{3}$千米.
如图,机车甲、乙分别停在A,B处,且AB=10km,甲的速度为4千米/小时,乙的速度是甲的$\frac{1}{2}$,甲沿北偏东60°的方向移动,乙沿正北方向移动,若两者同时移动100分钟,则它们之间的距离为$\frac{20\sqrt{3}}{3}$千米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 17 | C. | 19 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com