
分析 由题意可得数列的前10项为负数,从第11项开始为正数,且a10+a11>0,由等差数列的求和公式和性质逐个选项验证可得.
解答 解:∵等差数列{an}前n项和Sn有最小值,∴公差d>0,①正确,②错误;
又∵$\frac{{a}_{11}}{{a}_{10}}$<-1,∴a10<0,a11>0,且a10+a11>0,
∴等差数列{an}的前10项为负数,从第11项开始为正数,
∴当n=10时,Sn最小,④错误,⑤正确;
∴S19=$\frac{19({a}_{1}+{a}_{19})}{2}$=$\frac{19×2{a}_{10}}{2}$=19a10<0,
S20=$\frac{20({a}_{1}+{a}_{20})}{2}$=10(a10+a11)>0,
∴S1,S2…S19都小于零,S20,S21…都大于零,③正确.
故答案为:①③⑤
点评 本题考查等差数列的求和公式和性质,判定出数列项的正负变化是解决问题的关键,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
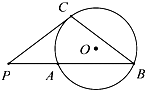 如图,PC是⊙O的切线,C为切点,PAB为割线,PC=2,PA=1,∠P=60°,则BC=( )
如图,PC是⊙O的切线,C为切点,PAB为割线,PC=2,PA=1,∠P=60°,则BC=( )| A. | 3 | B. | 2 | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com