Question

2．已知下列四个命题：
P₁：若直线l和平面α内无数条直线垂直，则l⊥α
P₂：若f（x）=2^x-2^-x，则?x∈R，f（-x）=-f（x）
P₃：在△ABC中，若A＞B，则sinA＞sinB
其中真命题的个数是（　　）

• A． 0
• B． 1
• C． 2
• D． 3

Answer 1

分析 举例说明命题P₁是假命题；
根据f（x）解析式判断P₂是真命题；
利用正弦定理判断P₃是真命题．

解答 解：对于命题P₁，直线l和平面α内无数条直线垂直，则l⊥α不一定成立，
如图所示：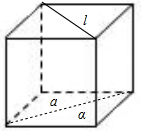

l⊥a，l垂直于α中平行与a的所有直线，但l与α不垂直，P₁是假命题；
对于命题P₂，f（x）=2^x-2^-x，则?x∈R，
f（-x）=2^-x-2^x=-（2^x-2^-x）=-f（x），∴P₂是真命题；
对于P₃，△ABC中，若A＞B，则有a＞b，
由正弦定理知a=2RsinA，b=2RsinB，
∴sinA＞sinB，∴P₃是真命题；
综上，以上真命题的个数是2．
故选：C．

点评 本题利用命题真假的判断考查了线面垂直，奇函数以及正弦定理的应用问题，是综合题．