
���� ��1�����ȰѲ�������ת����ֱ�����귽�̣���һ�����õ���������m��ֵ��
��2�����ã�1���Ľ��ۣ���һ������һ����Ϊ������һԪ���η��̣���һ�����ݸ���ϵ���Ĺ�ϵ��������Ĺ�ϵʽ�������ú�����ֵ����������
��� �⣺��1������ԲC��$\left\{\begin{array}{l}x=2cosϕ\\ y=\sqrt{3}sinϕ\end{array}\right.$����Ϊ����������ͨ����Ϊ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$�����̵���ΪF��
��F��-1��0����
��ֱ��l��$\left\{\begin{array}{l}{x=m+tcos��}\\{y=tsin��}\end{array}\right.$��tΪ����������k�У�k��Z������ͨ����Ϊ��y=tan����x-m����
�ߦ���k�У�k��Z��
��tan����0
��ֱ�߾�����F��
���ԣ�0=tan����-1-m������ã�m=-1��
��2����ֱ�ߵIJ�������$\left\{\begin{array}{l}x=-1+tcos��\\ y=tsin��\end{array}\right.$��tΪ������������ԲC����ͨ����$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$�������ã�
��3cos2��+4sin2����t2-6tcos��-9=0��
���A��B��ֱ�߲��������ж�Ӧ�IJ����ֱ�Ϊt1��t2��
��|FA|��|FB|=|t1t2|
=$\frac{9}{3{cos}^{2}��+4{sin}^{2}��}$
=$\frac{9}{3+{sin}^{2}��}$��
��sin��=��1ʱ��|FA|��|FB|����СֵΪ$\frac{9}{4}$��
���� ���⿼���֪ʶҪ�㣺�������̺�ֱ�����귽�̵Ļ��������������̵�Ӧ�ã�����ϵ���Ĺ�ϵ��Ӧ�ã����Ǻ�������ֵ�����Ӧ�ã���Ҫ����ѧ�����������Ͷ����ν�ϵ�����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�콭��ʡ��ɫ��У������ѧ������һ��ѧ�������Ծ��������棩 ���ͣ�ѡ����
����˵����ȷ���ǣ� ��
A�� ����
���� ���ǡ�
���ǡ� ���ı�Ҫ���������
���ı�Ҫ���������
B���� Ϊ�����⡱�ǡ�
Ϊ�����⡱�ǡ� Ϊ�����⡱�ı�Ҫ���������
Ϊ�����⡱�ı�Ҫ���������
C�����⡰ ��ʹ��
��ʹ�� ���ķ��ǣ���
���ķ��ǣ��� ��
�� ��
��
D������ ����
���� ��
��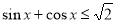 ������
������ ��������
��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | $\frac{\sqrt{3}}{2}$ | B�� | $\sqrt{3}$ | C�� | 2 | D�� | 2$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Ȳ����Ҳ����Ҫ���� | B�� | ��ֲ���Ҫ���� | ||
| C�� | ��Ҫ��������� | D�� | ��Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ԲO��һ��P��Բ������PC������PAB��CΪ�е㣮��֤��AP•BC=AC•CP��
��ͼ����ԲO��һ��P��Բ������PC������PAB��CΪ�е㣮��֤��AP•BC=AC•CP���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com