Question

17．双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点和虚轴上的一个端点分别为F，A，点P为双曲线C左支上一点，若△APF周长的最小值为6b，则双曲线C的离心率为（　　）

• A． $\frac{\sqrt{56}}{8}$
• B． $\frac{\sqrt{85}}{7}$
• C． $\frac{\sqrt{85}}{6}$
• D． $\frac{\sqrt{13}}{3}$

Answer 1

分析 由题意求得A，F的坐标，设出F'，运用双曲线的定义可得|PF|=|PF'|+2a，则△APF的周长为|PA|+|PF|+|AF|=|PA|+|PF'|+2a+$\sqrt{{b}^{2}+{c}^{2}}$，运用三点共线取得最小值，可得6a=7b，由a，b，c的关系，结合离心率公式，计算即可得到所求值．

解答 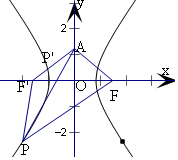解：由题意可得A（0，b），F（c，0），设F'（-c，0），
由双曲线的定义可得|PF|-|PF'|=2a，
|PF|=|PF'|+2a，
|AF|=|AF'|=$\sqrt{{b}^{2}+{c}^{2}}$，
则△APF的周长为|PA|+|PF|+|AF||=|PA|+|PF'|+2a+|AF'|
≥2|AF'|+2a，
当且仅当A，P，F'共线，取得最小值，且为2a+2$\sqrt{{b}^{2}+{c}^{2}}$，
由题意可得6b=2a+2$\sqrt{{b}^{2}+{c}^{2}}$，
即b=$\frac{6}{7}$a，
c=$\sqrt{{a}^{2}+{b}^{2}}$=$\frac{\sqrt{85}}{7}$a，
则e=$\frac{c}{a}$=$\frac{\sqrt{85}}{7}$，
故选：B．

点评 本题考查双曲线的离心率的求法，注意运用双曲线的定义和转化为三点共线取得最小值，考查运算能力，属于中档题．