
分析 (Ⅰ)有条件利用三角恒等变换化简函数的解析式,再利用正弦函数的周期性,求得结论.
(Ⅱ)令$2kπ+\frac{π}{2}≤2x+\frac{π}{6}≤2kπ+\frac{3π}{2},k∈Z$,求得x的范围,可得函数的单调减区间,再结合$x∈[0,\frac{π}{2}]$,得出结论.
解答 解:(Ⅰ)∵$f(x)=\sqrt{3}sinxcosx+{cos^2}x$$f(x)=\frac{{\sqrt{3}}}{2}sin2x+\frac{1+cos2x}{2}$$f(x)=(\frac{{\sqrt{3}}}{2}sin2x+\frac{1+cos2x}{2})$,
∴$f(x)=sin(2x+\frac{π}{6})+\frac{1}{2}$,故$T=\frac{2π}{|ω|}=\frac{2π}{2}=π$,即f(x)的最小正周期为π.
(Ⅱ)令$2kπ+\frac{π}{2}≤2x+\frac{π}{6}≤2kπ+\frac{3π}{2},k∈Z$,求得kπ+$\frac{π}{6}$≤x≤kπ+$\frac{2π}{3}$,
即f(x)的递减区间为:$[kπ+\frac{π}{6},kπ+\frac{2π}{3}],k∈Z$.
再结合$x∈[0,\frac{π}{2}]$,由$[0,\frac{π}{2}]∩[kπ+\frac{π}{6},kπ+\frac{2π}{3}]$=$[\frac{π}{6},+\frac{π}{2}]$,k∈Z,
所以f(x)的递减区间为$[\frac{π}{6},\frac{π}{2}]$.
点评 本题主要考查三角恒等变换,正弦函数的周期性、单调性,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
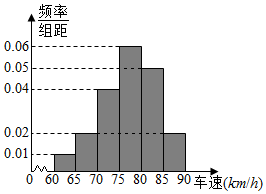 对高速公路某段上汽车行驶速度进行抽样调查,画出如图频率分布直方图.根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过80km/h的概率( )
对高速公路某段上汽车行驶速度进行抽样调查,画出如图频率分布直方图.根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过80km/h的概率( )| A. | 75,0.25 | B. | 80,0.35 | C. | 77.5,0.25 | D. | 77.5,0.35 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,+∞) | B. | [0,$\frac{1}{2}$] | C. | ($\frac{1}{2}$,4) | D. | (1,4] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com