
| A. | ① | B. | ①③ | C. | ①② | D. | ②③ |
分析 (1)根据正弦函数的单调性和诱导公式推导;
(2)由锐角三角形推出A的范围,利用正弦定理得出AC的范围;
(3)作AD⊥BC,利用向量线性运算的几何意义得出A,D,P三点共线.
解答 解:(1)若A$<B≤\frac{π}{2}$,则sinA<sinB,
若A$<\frac{π}{2}<B$<π,则A<π-B$<\frac{π}{2}$,∴sinA<sin(π-B)=sinB,故①正确
(2)由正弦定理得$\frac{BC}{sinA}=\frac{AC}{sinB}=\frac{AC}{2sinAcosA}$,∴AC=2BCcosA=2$\sqrt{3}$cosA.
∵△ABC为锐角三角形,∴$\left\{\begin{array}{l}{A<\frac{π}{2}}\\{2A<\frac{π}{2}}\\{π-A-2A<\frac{π}{2}}\end{array}\right.$,解得$\frac{π}{6}<A<\frac{π}{4}$.
∴$\sqrt{6}$<2$\sqrt{3}$cosA<3,故②错误.
(3)∵$\overrightarrow{OP}$=$\overrightarrow{OA}$+λ($\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|sinB}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|sinC}$),∴$\overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA}$=λ($\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|sinB}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|sinC}$).
作△ABC的BC边上的高AD,则$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|sinB}$=k1$\overrightarrow{AD}$,$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|sinC}$=k2$\overrightarrow{AD}$,
∴$\overrightarrow{AP}$=m$\overrightarrow{AD}$,即点P在直线AD上,故③错误.
故选:A.
点评 本题考查了正弦定理,平面向量线性运算的几何意义,属于中档题.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{2}$ | B. | kπ(k∈Z) | C. | 2kπ-$\frac{π}{2}$(k∈Z) | D. | 2(k+1)π+$\frac{3π}{2}$(k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
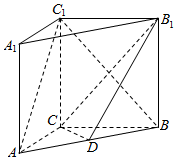 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com