
分析 (1)由已知条件得f(-x)+f(x)=0,化简求解m即可.
(2)利用$f(x)={log_a}\frac{1+x}{x-1}$,通过换元法,结合当x1>x2>1时,判断函数的单调性,当a>1时,当0<a<1时,判断函数的单调性.
(3)求出函数f(x)的定义域,通过0<a<1.f(x)在(a-2,n)为增函数,列出方程,a>1,列出方程求解即可.
解答 解:(1)由已知条件得f(-x)+f(x)=0对定义域中的x均成立.
∴${log_a}\frac{mx+1}{-x-1}+{log_a}\frac{1-mx}{x-1}=0$,
即$\frac{mx+1}{-x-1}•\frac{1-mx}{x-1}=1$…(1分)
∴m2x2-1=x2-1对定义域中的x均成立.m2=1,即m=1(舍去)或m=-1.…(3分)
(2)由(1)得$f(x)={log_a}\frac{1+x}{x-1}$,设$t=\frac{x+1}{x-1}=\frac{x-1+2}{x-1}=1+\frac{2}{x-1}$,
∴当x1>x2>1时,${t_1}-{t_2}=\frac{2}{{{x_1}-1}}-\frac{2}{{{x_2}-1}}=\frac{{2({x_2}-{x_1})}}{{({x_1}-1)({x_2}-1)}}$,∴t1<t2.…(4分)
当a>1时,logat1<logat2,即f(x1)<f(x2).…(5分)
∴当a>1时,f(x)在(1,+∞)上是减函数.…(6分)
同理当0<a<1时,f(x)在(1,+∞)上是增函数.…(7分)
(3)∵函数f(x)的定义域为(-∞,-1)∪(1,+∞),
∴①a-2<n≤-1,∴0<a<1.∴f(x)在(a-2,n)为增函数,要使值域为(1,+∞),
有$\left\{\begin{array}{l}\frac{1+n}{n-1}=0\\ \frac{1+(a-2)}{(a-2)-1}=a\end{array}\right.$解得:n=-1,$a=2-\sqrt{3}$($a=2+\sqrt{3}$不符题意,舍去)…(9分)
?1≤a-2<n∈Z,∴a>2.∴f(x)在(a-2,n)为减函数,要使值域为(1,+∞),
有$\left\{\begin{array}{l}\frac{1+n}{n-1}=a\\ a-2=1\end{array}\right.$解得:n=2,a=3…(11分)
综上n=-1,$a=2-\sqrt{3}$或n=2,a=3…(12分)
点评 本题考查函数与方程的综合应用,函数的单调性以及函数的最值的求法,考查转化思想以及计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
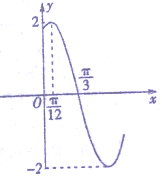 f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)的图象,则g(x)的单调递增区间为( )
f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)的图象,则g(x)的单调递增区间为( )| A. | [-$\frac{5π}{12}$+kπ,$\frac{π}{12}$+kπ](k∈Z) | B. | [-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z) | ||
| C. | [-$\frac{π}{12}$+kπ,$\frac{5π}{12}$+kπ](k∈Z) | D. | [-$\frac{π}{6}$+kπ,$\frac{5π}{6}$+kπ](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com