练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    过圆x2+y2+2x-4y=0的圆心，且与直线2x+3y=0垂直的直线方程为
     
    ．
    考点：圆的一般方程
    专题：直线与圆
    分析：求出圆的圆心，以及直线的斜率，利用点斜式方程即可得到直线的方程．
    解答： 解：∵圆的标准方程为（x+1）2+（y-2）2=5，
    ∴圆心坐标为（-1，2），
    直线2x+3y=0的斜率k=-
    2
    3
    ，
    则与直线2x+3y=0垂直的直线斜率k=
    3
    2
    ，
    ∴所求的直线方程为y-2=
    3
    2
    （x+1），
    即3x-2y+7=0，
    故答案为：3x-2y+7=0
    点评：本题主要考查直线方程的求法，求出圆心坐标以及直线斜率是解决本题的关键，比较基础．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    以下四个命题：
    ①命题“若x2-3x+2=0，则x=1”的逆否命题为“若x≠1，则x2-3x+2≠0”；
    ②设函数f（x）=x+ln（x+
    		1+x2
    ），则对于任意实数a和b，“a+b＜0”是“f（a）+f（b）＜0”的充要条件；
    ③命题p：“?x∈R，x2+x+1＜0”，则命题p的否定为“?x∈R，x2+x+1≥0”；
    ④在△ABC中，A＜B是sinA＜sinB的充分不必要条件；
    其中真命题为（　　）
    A、①B、①②
    C、①②③D、①②③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

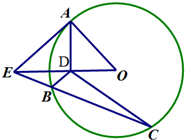    如图，AE是圆O的切线，A是切点，AD⊥OE于D，割线EC交圆O于B、C两点．
    （Ⅰ）证明：O，D，B，C四点共圆；
    （Ⅱ）设∠DBC=50°，∠ODC=30°，求∠OEC的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设等差数列{an}的前n项和为Sn．且S4=4S2，a2n=2an+1．
    （1）求数列{an}的通项公式；
    （2）若an=2n-1，数列{bn}满足：b1=3，bn-bn-1=an+1（n≥2），求数列{
    1
    bn
    }    的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

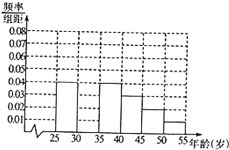    某同学在寒假期间进行社会实践活动，对[25，55]岁的人群随机抽取行人进行了一次生活习惯是否符合环保观念的调查，若生活习惯符合环保观念的称为“环保族”，否则称为“非环保族”，得到如下统计表和各年龄段人数的频率分布直方图：
    组数 分组 环保数的人数 占本组的频率
    第一组 [25，30） 120 0.6
    第二组 [30，35） 195 p
    第三组 [35，40） 100 0.5
    第四组 [40，45） a 0.4
    第五组 [45，50） 30 0.3
    第六组 [50，55] 15 0.3
    （Ⅰ）补全频率分布直方图，并求n、a、p的值；
    （Ⅱ）从[35，45）岁年龄段的“环保族”中采用分层抽样法抽取16人参加户外环保体验活动，其中选取3人作为领队，记选取的3名领队中年龄在[35，40）岁的人数为X，求随机变量X的分布列和数学期望EX．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知a＞b＞0，ab=1，则
    a2+b2
    a-b
    的最小值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设Sn为数列{an}的前n项和，数列{an}满足a1=1，a2=1，且[3+(-1)n]an+2=2an-2[(-1)n-1]（n=1，2，3，…）． 则S100=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设x，y满足约束条件
    3x-y-6≤0
    x-y+2≥0
    x≥0
    y≥0
    ，则目标函数z=2x+y最大值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某商场为了了解顾客的购物信息，随机的在商场收集了100位顾客购物的相关数据，整理如下：
    一次购物款（单位：元）[0，50）[50，100）[100，150）[150，200）[200，+∞）
    顾客人数m2030n10
    统计结果显示100位顾客中购物款不低于100元的顾客占60%，据统计该商场每日大约有5000名顾客，为了增加商场销售额度，对一次性购物不低于100元的顾客发放纪念品（每人一件）．（注：视频率为概率）
    （Ⅰ）试确定m，n的值，并估计该商场每日应准备纪念品的数量；
    （Ⅱ）为了迎接店庆，商场进行让利活动，一次购物款200元及以上的一次返利30元；一次性购物款小于200元的按购物款的百分比返利，具体见下表：
    一次购物款（单位：元）[0，50）[50，100）[100，150）[150，200）
    返利百分比06%8%10%
    请估计该商场日均让利多少元？

    查看答案和解析>>

    同步练习册答案