
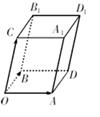
 ,BC=1,AC=CC1=2.
,BC=1,AC=CC1=2.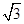 ,求二面角A1-AB-C的大小.
,求二面角A1-AB-C的大小.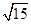 .
.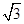 ,然后证明∠A1FD为二面角A1-AB-C的平面角,求出tan∠A1FD=
,然后证明∠A1FD为二面角A1-AB-C的平面角,求出tan∠A1FD=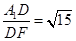 即可.
即可. 平面AA1C1C,故平面AA1C1C⊥平面ABC,又BC⊥AC,所以BC⊥平面AA1C1C,连结A1C,因为侧面AA1C1C是棱形,所以AC1⊥A1C,由三垂线定理的AC1⊥A1B.
平面AA1C1C,故平面AA1C1C⊥平面ABC,又BC⊥AC,所以BC⊥平面AA1C1C,连结A1C,因为侧面AA1C1C是棱形,所以AC1⊥A1C,由三垂线定理的AC1⊥A1B.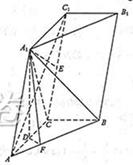
 平面BCC1B1,故平面AA1C1C⊥平面BCC1B1,
平面BCC1B1,故平面AA1C1C⊥平面BCC1B1,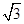 ,因为A1C为∠ACC1的平分线,故A1D=A1E=
,因为A1C为∠ACC1的平分线,故A1D=A1E=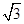 ,
, ,得D为AC的中点,DF=
,得D为AC的中点,DF=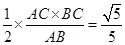 ,tan∠A1FD=
,tan∠A1FD=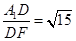 ,所以二面角A1-AB-C的大小为arctan
,所以二面角A1-AB-C的大小为arctan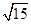 .
. (-2,1,0),
(-2,1,0),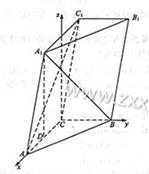
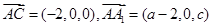 ,
,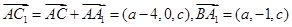 ,由
,由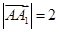 得
得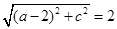 ,即
,即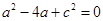 ,于是
,于是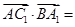
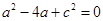 ①,所以
①,所以 .
. ,则
,则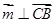 ,
,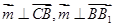 ,即
,即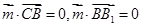 ,因
,因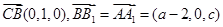 ,故y=0,且(a-2)x-cz=0,令x=c,则z=2-a,
,故y=0,且(a-2)x-cz=0,令x=c,则z=2-a, ,点A到平面BCC1B1的距离为
,点A到平面BCC1B1的距离为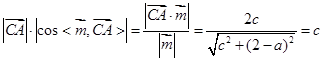 ,又依题设,点A到平面BCC1B1的距离为
,又依题设,点A到平面BCC1B1的距离为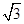 ,所以c=
,所以c= 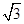 .代入①得a=3(舍去)或a=1.于是
.代入①得a=3(舍去)或a=1.于是 ,
,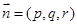 ,则
,则 ,即
,即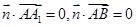 .
. 且-2p+q=0,令p=
且-2p+q=0,令p=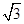 ,则q=2
,则q=2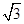 ,r=1,
,r=1, ,又
,又 为平面ABC的法向量,故cos
为平面ABC的法向量,故cos ,所以二面角A1-AB-C的大小为arccos
,所以二面角A1-AB-C的大小为arccos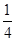 ,
,

科目:高中数学 来源:不详 题型:解答题
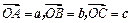 ,可构成空间向量的一个基底,若
,可构成空间向量的一个基底,若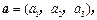
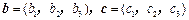 ,在向量已有的运算法则的基础上,新定义一种运算
,在向量已有的运算法则的基础上,新定义一种运算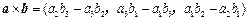 ,显然
,显然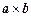 的结果仍为一向量,记作
的结果仍为一向量,记作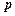 .
.
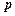 为平面
为平面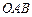 的法向量;
的法向量;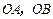 为边的平行四边形
为边的平行四边形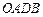 的面积等于
的面积等于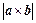 ;
;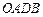 按向量
按向量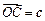 平移,得到一个平行六面体
平移,得到一个平行六面体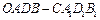 ,试判断平行六面体的体积
,试判断平行六面体的体积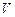 与
与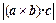 的大小.
的大小.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
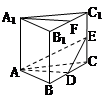
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
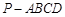 ,底面
,底面 为矩形,侧棱
为矩形,侧棱 ,其中
,其中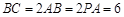 ,
,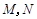 为侧棱
为侧棱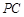 上的两个三等分点,如下图所示.
上的两个三等分点,如下图所示.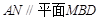 ;
;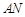 与
与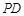 所成角的余弦值;
所成角的余弦值;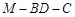 的余弦值.
的余弦值.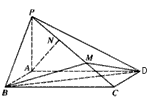
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.平面ABC⊥平面ABD |
| B.平面ABD⊥平面BDC |
| C.平面ABC⊥平面BDE,且平面ADC⊥平面BDE |
| D.平面ABC⊥平面ADC,且平面ADC⊥平面BDE |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com