
分析 画出约束条件的可行域,利用目标函数的最值得到a,b的关系式,利用基本不等式求解最值即可.
解答 解:约束条件$\left\{\begin{array}{l}{x-y+2≥0}\\{4x-y-4≤0}\\{x≥0}\\{y≥0}\end{array}\right.$的可行域如图,有可行域可知:z=ax+by(a>0,b>0)在(2,4)点取得最大值,故2a+4b=6,即a+2b=3,3=a+2b=a+b+b≥3$\root{3}{abb}$≥3$\frac{3}{\frac{1}{a}+\frac{1}{b}+\frac{1}{b}}$=$\frac{9}{\frac{1}{a}+\frac{2}{b}}$,所以$\frac{1}{a}+\frac{2}{b}$≥3,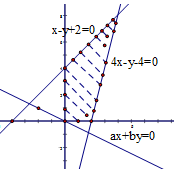 ,则${log}_{\sqrt{3}}(\frac{1}{a}+\frac{2}{b})$≥$lo{g}_{\sqrt{3}}3$=2.
,则${log}_{\sqrt{3}}(\frac{1}{a}+\frac{2}{b})$≥$lo{g}_{\sqrt{3}}3$=2.
故答案为:2.
点评 本题考查线性规划的应用,基本不等式的应用,考查转化思想以及计算能力.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin($\frac{x}{2}$-$\frac{π}{8}$) | B. | y=sin($\frac{x}{2}$+$\frac{π}{8}$) | C. | y=sin(2x-$\frac{π}{8}$) | D. | y=sin(2x-$\frac{π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
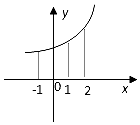 已知函数y=f(x)的图象如图所示,设函数y=f(x)从-1到1的平均变化率为v1,从1到2的平均变化率为v2,则v1与v2的大小关系为( )
已知函数y=f(x)的图象如图所示,设函数y=f(x)从-1到1的平均变化率为v1,从1到2的平均变化率为v2,则v1与v2的大小关系为( )| A. | v1>v2 | B. | v1=v2 | C. | v1<v2 | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com