
若函数 ,非零向量
,非零向量 ,我们称
,我们称 为函数
为函数 的“相伴向量”,
的“相伴向量”, 为向量
为向量 的“相伴函数”.
的“相伴函数”.
(1)已知函数 的最小正周期为
的最小正周期为 ,求函数
,求函数 的“相伴向量”;
的“相伴向量”;
(2)记向量 的“相伴函数”为
的“相伴函数”为 ,将
,将 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移 个单位长度,得到函数
个单位长度,得到函数 ,若
,若 ,求
,求 的值;
的值;
(3)对于函数 ,是否存在“相伴向量”?若存在,求出
,是否存在“相伴向量”?若存在,求出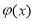 “相伴向量”;
“相伴向量”;
若不存在,请说明理由.
(1)(1,1);(2)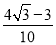 ;(3)不存在“相伴向量”
;(3)不存在“相伴向量”
【解析】
试题分析:(1)由函数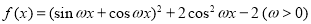 平方项展开化简,再通过化一公式即可得一个函数的形式,又因为最小正周期为
平方项展开化简,再通过化一公式即可得一个函数的形式,又因为最小正周期为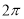 ,即可求得
,即可求得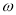 的值.再将函数展开写成
的值.再将函数展开写成 的形式及可得结论.
的形式及可得结论.
(2)由向量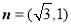 为函数
为函数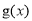 的“相伴向量”,所以可得到函数
的“相伴向量”,所以可得到函数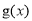 .再将
.再将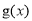 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移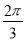 个单位长度,得到函数
个单位长度,得到函数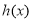 .再根据
.再根据 .通过解三角方程即可得到所求的结论.
.通过解三角方程即可得到所求的结论.
(3)对于函数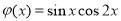 ,是否存在“相伴向量”.通过反证法的思想,可证明不存在函数
,是否存在“相伴向量”.通过反证法的思想,可证明不存在函数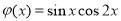 的“相伴向量”.
的“相伴向量”.
(1)
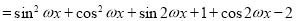
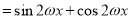
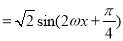 , 1分
, 1分
依题意得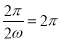 ,故
,故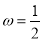 . 2分
. 2分
∴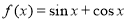 ,即
,即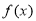 的“相伴向量”为(1,1). 3分
的“相伴向量”为(1,1). 3分
(2)依题意,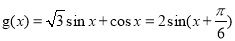 , 4分
, 4分
将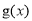 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),
得到函数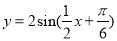 , 5分
, 5分
再将所得的图象上所有点向左平移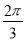 个单位长度,得到
个单位长度,得到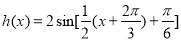 ,
,
即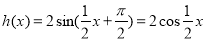 , 6分
, 6分
∵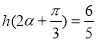 ,∴
,∴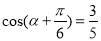 ,
,
∵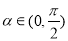 ,∴
,∴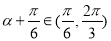 ,∴
,∴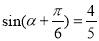 , 8分
, 8分
∴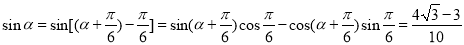 . 10分
. 10分
(3)若函数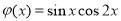 存在“相伴向量”,
存在“相伴向量”,
则存在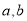 ,使得
,使得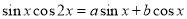 对任意的
对任意的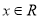 都成立, 11分
都成立, 11分
令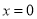 ,得
,得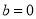 ,
,
因此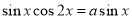 ,即
,即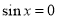 或
或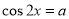 ,
,
显然上式对任意的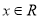 不都成立,
不都成立,
所以函数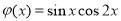 不存在“相伴向量”. 13分
不存在“相伴向量”. 13分
(注:本题若化成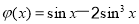 ,直接说明不存在的,给1分)
,直接说明不存在的,给1分)
考点:1.三角函数的性质.2.三角恒等变换.3.三角函数的图象.4.新定义问题.5.反正的思想.


 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源:2013-2014学年福建省高考考前模拟文科数学试卷(解析版) 题型:选择题
已知函数 ,如果在区间
,如果在区间 上存在
上存在 个不同的数
个不同的数 使得比值
使得比值 成立,则
成立,则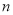 的取值构成的集合是( )
的取值构成的集合是( )
A. B.
B.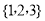 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省厦门市高三5月适应性考试理科数学试卷(解析版) 题型:选择题
如图,棱长为 的正方体
的正方体 中,
中, 为线段
为线段 上的动点,则下列结论错误的是
上的动点,则下列结论错误的是

A.
B.平面 平面
平面
C. 的最大值为
的最大值为
D. 的最小值为
的最小值为
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省三明市高三5月质量检查理科数学试卷(解析版) 题型:填空题
已知矩形的周长为36,矩形绕它的一条边旋转形成一个圆柱,则旋转形成的圆柱的侧面积的最
大值为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省三明市高三5月质量检查理科数学试卷(解析版) 题型:选择题
已知双曲线 与椭圆
与椭圆 有相同的焦点,则该双曲线的渐近线方程为( )
有相同的焦点,则该双曲线的渐近线方程为( )
A.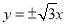 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省三明市高三5月质量检查文科数学试卷(解析版) 题型:选择题
设函数 的导函数为
的导函数为 ,那么下列说法正确的是( )
,那么下列说法正确的是( )
A.若 ,则
,则 是函数
是函数 的极值点
的极值点
B. 若 是函数
是函数 的极值点,则
的极值点,则
C. 若 是函数
是函数 的极值点,则
的极值点,则 可能不存在
可能不存在
D.若 无实根 ,则函数
无实根 ,则函数 必无极值点
必无极值点
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省武威市高三数学专题训练选择填空限时练六(解析版) 题型:选择题
已知 =2+i,则复数z的共轭复数为( )
=2+i,则复数z的共轭复数为( )
A.3+i B.3-I C.-3-i D.-3+i
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com