
(本小题满分12分)已知函数 ,其中常数
,其中常数 .
.
(1)当 时,求函数
时,求函数 的极大值;
的极大值;
(2)试讨论 在区间
在区间 上的单调性;
上的单调性;
(3)当 时,曲线
时,曲线 上总存在相异两点
上总存在相异两点 ,
, ,使得曲线
,使得曲线 在点
在点 处的切线互相平行,求
处的切线互相平行,求 的取值范围.
的取值范围.
(1)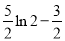 ;
;
(2)当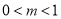 时,
时,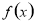 在
在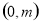 上单调递减,在
上单调递减,在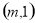 上单调递增,
上单调递增,
当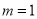 时,
时,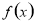 在
在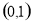 单调递减,当
单调递减,当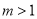 时,
时,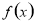 在
在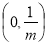 上单调递减,在
上单调递减,在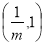 上单调递增;
上单调递增;
(3)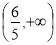 .
.
【解析】
试题分析:(1)求函数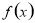 的极值的一般步骤:(1)确定函数的定义域;(2)求导数
的极值的一般步骤:(1)确定函数的定义域;(2)求导数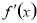 ;(3)解方程
;(3)解方程 ,求出函数定义域内的所有根;(4)列表检验
,求出函数定义域内的所有根;(4)列表检验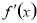 在
在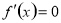 的根
的根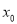 左右两侧的符号,如果在
左右两侧的符号,如果在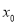 附近的左侧
附近的左侧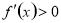 ,右侧
,右侧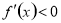 ,那么
,那么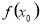 是极大值;如果在
是极大值;如果在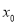 附近的左侧
附近的左侧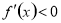 ,右侧
,右侧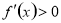 ,那么
,那么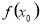 是极小值;(2)函数
是极小值;(2)函数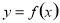 在某个区间内可导,则若
在某个区间内可导,则若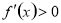 ,则
,则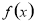 在这个区间内单调递增,若
在这个区间内单调递增,若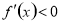 ,则
,则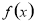 在这个区间内单调递减;(3)对于恒成立的问题,常用到两个结论:(1)
在这个区间内单调递减;(3)对于恒成立的问题,常用到两个结论:(1)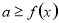 恒成立
恒成立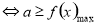 ,(2)
,(2)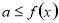 恒成立
恒成立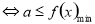 .
.
试题解析:(1)当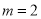 时,
时,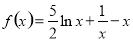 ,
,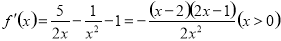 ,
,
由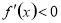 得
得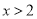 或
或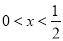 ,由
,由 得
得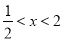 ,因此函数
,因此函数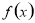 在区间
在区间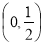 和
和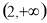 单调递减,在区间
单调递减,在区间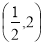 上单调递增,故
上单调递增,故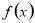 的极大值为
的极大值为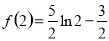

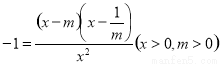
当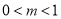 时,
时,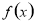 在
在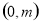 上单调递减,在
上单调递减,在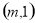 上单调递增
上单调递增
当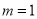 时,
时,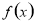 在
在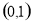 单调递减
单调递减
当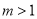 时,
时,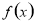 在
在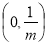 上单调递减,在
上单调递减,在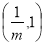 上单调递增
上单调递增
(3)由题意,可得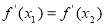 (
(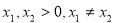 )
)
既
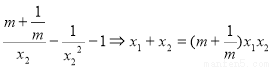
 对
对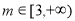 恒成立
恒成立
另 则
则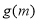 在
在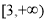 上单调递增,
上单调递增,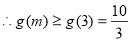
故 ,从而
,从而
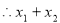 的取值范围是
的取值范围是 .
.
考点:1、利用导数求函数极值;2、利用导数求函数的单调性;3、恒成立的问题.
考点分析: 考点1:导数及其应用 试题属性

 考前必练系列答案
考前必练系列答案科目:高中数学 来源:2014-2015学年广东省汕头市高三第一次模拟考试理科数学试卷(解析版) 题型:解答题
(本小题满分14分)在平面直角坐标系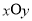 中,已知动点
中,已知动点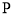 到两个定点
到两个定点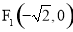 ,
,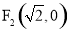 的距离的和为定值
的距离的和为定值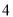 .
.
(1)求点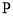 运动所成轨迹
运动所成轨迹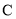 的方程;
的方程;
(2)设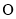 为坐标原点,若点
为坐标原点,若点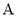 在轨迹
在轨迹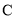 上,点
上,点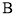 在直线
在直线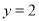 上,且
上,且 ,试判断直线
,试判断直线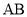 与圆
与圆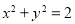 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省兰州市高三诊断考试理科数学试卷(解析版) 题型:选择题
已知不等式组 所表示的平面区域为
所表示的平面区域为 ,若直线
,若直线 与平面区域
与平面区域 有公共点,则
有公共点,则 的取值范围为是
的取值范围为是
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高三第一次联考文科数学试卷(解析版) 题型:选择题
已知函数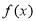 的定义域为
的定义域为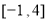 ,部分对应值如下表,
,部分对应值如下表,

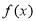 的导函数
的导函数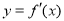 的图象如右图所示.当
的图象如右图所示.当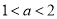 时,函数
时,函数 的零点的个数为( )
的零点的个数为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高三第一次联考理科数学试卷(解析版) 题型:填空题
在平面直角坐标系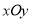 中,圆
中,圆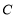 的方程为
的方程为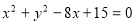 ,若直线
,若直线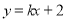 上至少存在一点,使得以该点为圆心,半径为
上至少存在一点,使得以该点为圆心,半径为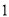 的圆与圆
的圆与圆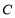 有公共点,则
有公共点,则 的最小值是____.
的最小值是____.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省福州市高三毕业班第六次质量检查理科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知函数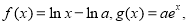 其中
其中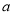 为常数,函数
为常数,函数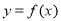 和
和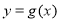 的图象在它们与坐标轴交点的切线互相平行.
的图象在它们与坐标轴交点的切线互相平行.
(Ⅰ)求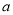 的值;
的值;
(Ⅱ)求函数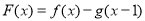 的单调区间;
的单调区间;
(Ⅲ)若不等式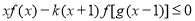 在区间
在区间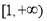 上恒成立,求实数
上恒成立,求实数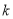 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com