
分析 x>0时,求f′(x),并容易判断出f′(x)>0,所以f(x)在(0,+∞)上是单调函数.然后判断有没有x1,x2使得f(x1)f(x2)<0:分别取x=2017-2017,1,便可判断f(2017-2017)<0,f(1)>0,从而得到f(x)在(0,+∞)上有一个零点,根据奇函数的对称性便得到f(x)在(-∞,0)上有一个零点,而因为f(x)是奇函数,所以f(0)=0,这样便得到在R上f(x)零点个数为3.
解答 解:x>0时,f′(x)=2017xln2017+$\frac{1}{xln2017}$>0,∴f(x)在(0,+∞)上单调递增,
取x=2017-2017,则f(2017-2017)=$201{7}^{\frac{1}{2017}}$-2017<0,又f(1)=2017>0;
∴f(x)在(0,+∞)上有一个零点,根据奇函数关于原点对称,f(x)在(-∞,0)也有一个零点;
又f(0)=0;
∴函数f(x)在R上有3个零点.
故答案为:3.
点评 考查奇函数的概念,函数导数符号和函数单调性的关系,函数零点的概念,以及判断函数在一区间上有没有零点,以及有几个零点的方法,奇函数图象关于原点的对称性.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
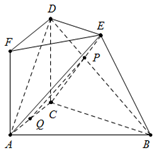 如图所示的多面体中,四边形ACDF为矩形,且平面ACDF⊥平面BCDE,平面ACDF⊥平面ABC,BC=2DE,DE∥BC,CE∩BD=P.
如图所示的多面体中,四边形ACDF为矩形,且平面ACDF⊥平面BCDE,平面ACDF⊥平面ABC,BC=2DE,DE∥BC,CE∩BD=P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | $\frac{5}{6}$ | D. | -$\frac{7}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
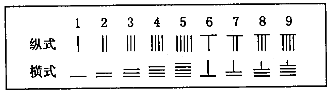
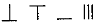 ,则5288用算筹式可表示为( )
,则5288用算筹式可表示为( )| A. | 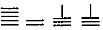 | B. | 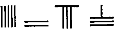 | C. | 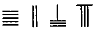 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $-\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com