
| A. | $\frac{3}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $-\frac{4}{5}$ |
分析 由题意可得f($\frac{π}{2}$)=f($\frac{3π}{2}$),化简可得tanφ的值,再根据cos2φ=$\frac{{cos}^{2}φ{-sin}^{2}φ}{{cos}^{2}φ{+sin}^{2}φ}$=$\frac{1{-tan}^{2}φ}{1{+tan}^{2}φ}$,计算求的结果.
解答 解:∵函数f(x)=sin(x+φ)-2cos(x+φ)(0<φ<π)的图象关于直线x=π对称,
∴f($\frac{π}{2}$)=f($\frac{3π}{2}$),即 cosφ+2sinφ=-cosφ-2sinφ,即cosφ=-2sinφ,即tanφ=-$\frac{1}{2}$,
则cos2φ=$\frac{{cos}^{2}φ{-sin}^{2}φ}{{cos}^{2}φ{+sin}^{2}φ}$=$\frac{1{-tan}^{2}φ}{1{+tan}^{2}φ}$=$\frac{1-\frac{1}{4}}{1+\frac{1}{4}}$=$\frac{3}{5}$,
故选:A.
点评 本题主要考查三角函数的图象的对称性,同角三角函数的基本关系、二倍角公式的应用,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| A. | 7.2万元 | B. | 7.35万元 | C. | 7.45万元 | D. | 7.5万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>4 | B. | a≥4 | C. | a≥0 | D. | a>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
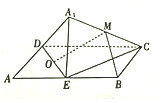 如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD).若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD).若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )| A. | 与平面A1DE垂直的直线必与直线BM垂直 | |
| B. | 过E作EG∥BM,G∈平面A1DC,则∠A1EG为定值 | |
| C. | 一定存在某个位置,使DE⊥MO | |
| D. | 三棱锥A1-ADE外接球半径与棱AD的长之比为定值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com