
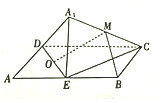
 如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD).若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD).若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )| A. | 与平面A1DE垂直的直线必与直线BM垂直 | |
| B. | 过E作EG∥BM,G∈平面A1DC,则∠A1EG为定值 | |
| C. | 一定存在某个位置,使DE⊥MO | |
| D. | 三棱锥A1-ADE外接球半径与棱AD的长之比为定值 |
分析 对于A,延长CB,DE交于H,连接A1H,运用中位线定理和线面平行的判定定理,可得BM∥平面A1DE,即可判断A;
对于B,运用平行线的性质和解三角形的余弦定理,以及异面直线所成角的定义,即可判断B;
对于C,连接A1O,运用线面垂直的判定定理和性质定理,可得AC与DE垂直,即可判断C;
对于D,由直角三角形的性质,可得三棱锥A1-ADE外接球球心为O,即可判断D.
解答 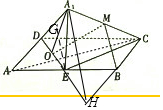 解:对于A,延长CB,DE交于H,连接A1H,由E为AB的中点,
解:对于A,延长CB,DE交于H,连接A1H,由E为AB的中点,
可得B为CH的中点,又M为A1C的中点,可得BM∥A1H,BM?平面A1DE,
A1H?平面A1DE,则BM∥平面A1DE,故与平面A1DE垂直的直线必与直线BM垂直,则A正确;
对于B,设AB=2AD=2a,过E作EG∥BM,G∈平面A1DC,
则∠A1EG=∠EA1H,
在△EA1H中,EA1=a,EH=DE=$\sqrt{2}$a,A1H=$\sqrt{{a}^{2}+2{a}^{2}-2•a•\sqrt{2}a•(-\frac{\sqrt{2}}{2})}$
=$\sqrt{5}$a,则∠EA1H为定值,即∠A1EG为定值,则B正确;
对于C,连接A1O,可得DE⊥A1O,若DE⊥MO,即有DE⊥平面A1MO,
即有DE⊥A1C,由A1C在平面ABCD中的射影为AC,
可得AC与DE垂直,但AC与DE不垂直.
则不存在某个位置,使DE⊥MO,则C不正确;
对于D,连接OA,由直角三角形斜边的中线长为斜边的一半,可得
三棱锥A1-ADE外接球球心为O,半径为$\frac{\sqrt{2}}{2}$a,
即有三棱锥A1-ADE外接球半径与棱AD的长之比为定值.则D正确.
故选:C.
点评 本题以命题的真假判断与应用为载体,考查了线面、面面平行与垂直的判定和性质定理,考查空间想象能力和推理能力,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $-\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | [0,1] | C. | [0,e] | D. | [-1,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}+1}{2}$ | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\sqrt{3}$-1 | D. | $\frac{\sqrt{5}-1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 5 | C. | 7 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,16] | B. | [6,14] | C. | [4,16] | D. | [$\sqrt{13}$,3$\sqrt{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
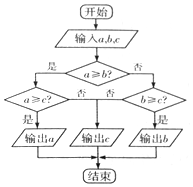
| A. | c | B. | b | C. | a | D. | $\frac{a+b+c}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com