
| A. | [1,16] | B. | [6,14] | C. | [4,16] | D. | [$\sqrt{13}$,3$\sqrt{5}$] |
分析 求出P,Q的轨迹方程,结合图象得出|$\overrightarrow{CP}$+$\overrightarrow{CQ}$|的最值.
解答 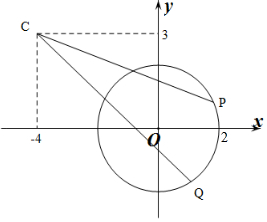 解:设P(x,y),则|PA|=$\sqrt{(x+4)^{2}+{y}^{2}}$,
解:设P(x,y),则|PA|=$\sqrt{(x+4)^{2}+{y}^{2}}$,
|PB|=$\sqrt{(x+1)^{2}+{y}^{2}}$,
∵|PA|=2|PB|,∴(x+4)2+y2=4(x+1)2+4y2,
即x2+y2=4,
∴P点在以原点为圆心,以2为半径的圆上,
同理可得Q也在原点为圆心,以2为半径的圆上,
∴当PQ重合且C,O,P三点共线时,|$\overrightarrow{CP}$+$\overrightarrow{CQ}$|取得最值,
∴|$\overrightarrow{CP}$+$\overrightarrow{CQ}$|的最大值为2(CO+2)=14,|$\overrightarrow{CP}$+$\overrightarrow{CQ}$|的最小值为2(CO-2)=6.
故选B.
点评 本题考查了平面向量的几何运算,轨迹方程的求解,属于中档题.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:选择题
| A. | 向右平行移动$\frac{5π}{12}$个单位长度 | B. | 向左平行移动$\frac{5π}{12}$个单位长度 | ||
| C. | 向右平行移动$\frac{5π}{6}$个单位长度 | D. | 向左平行移动$\frac{5π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
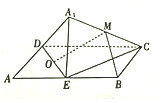 如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD).若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD).若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )| A. | 与平面A1DE垂直的直线必与直线BM垂直 | |
| B. | 过E作EG∥BM,G∈平面A1DC,则∠A1EG为定值 | |
| C. | 一定存在某个位置,使DE⊥MO | |
| D. | 三棱锥A1-ADE外接球半径与棱AD的长之比为定值 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4+2$\sqrt{3}$ | B. | 4-2$\sqrt{3}$ | C. | $\sqrt{3}$-1 | D. | $\sqrt{3}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
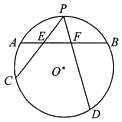 如图,已知AB为圆O的一条弦,点P为弧$\widehat{AB}$的中点,过点P任作两条弦PC,PD分别交AB于点E,F
如图,已知AB为圆O的一条弦,点P为弧$\widehat{AB}$的中点,过点P任作两条弦PC,PD分别交AB于点E,F查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | (4,+∞) | C. | (-∞,-2] | D. | (-∞,4] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com