
| A. | [0,+∞) | B. | [0,1] | C. | [0,e] | D. | [-1,0] |
分析 令f(x)=ln(x+2)+a(x2+x),x∈[-1,+∞),讨论a的范围,判断f(x)的单调性,得出fmin(x),令fmin(x)≥0即可.
解答 解:令f(x)=ln(x+2)+a(x2+x),x∈[-1,+∞),
∵不等式ln(x+2)+a(x2+x)≥0对于任意的x∈[-1,+∞)恒成立,
∴fmin(x)≥0,
f′(x)=$\frac{1}{x+2}$+2ax+a=$\frac{2a{x}^{2}+5ax+2a+1}{x+2}$,
令g(x)=2ax2+5ax+2a+1,
(1)若a=0,则g(x)=1,∴f′(x)>0,
∴f(x)在[-1,+∞)上单调递增,∴fmin(x)=f(-1)=0,符合题意;
(2)若a>0,则g(x)的图象开口向上,对称轴为x=-$\frac{5}{4}$,
∴g(x)在[-1,+∞)上单调递增,∴gmin(x)=g(-1)=1-a,
①若1-a≥0,即0<a≤1,则g(x)≥0,∴f′(x)≥0,由(1)可知符合题意;
②若1-a<0,即a>1,则存在x0∈(-1,+∞),
使得当x∈(-1,x0)时,g(x)<0,当x∈(x0,+∞)时,g(x)>0,
∴f(x)在(-1,x0)上单调递减,在(x0,+∞)上单调递增,
∴fmin(x)<f(-1)=0,不符合题意;
(3)若a<0,则g(x)的图象开口向下,对称轴为x=-$\frac{5}{4}$,
∴g(x)在[-1,+∞)上单调递减,gmax(x)=g(-1)=1-a>0,
∴存在x1∈(-1,+∞),使得当x∈(-1,x1)时,g(x)>0,当x∈(x1,+∞)时,g(x)<0,
∴f(x)在(-1,x1)单调递增,在(x1,+∞)上单调递减,
∴f(x)在(-1,+∞)上不存在最小值,不符合题意;
综上,a的取值范围是[0,1].
故选B.
点评 本题考查了导数与函数单调性的关系,函数恒成立问题研究及函数最值计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| A. | 7.2万元 | B. | 7.35万元 | C. | 7.45万元 | D. | 7.5万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
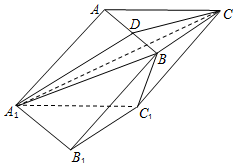 如图,在底边为等边三角形的斜三棱柱ABC-A1B1C1中,AA1=$\sqrt{3}$AB,四边形B1C1CB为矩形,过A1C做与直线BC1平行的平面A1CD交AB于点D.
如图,在底边为等边三角形的斜三棱柱ABC-A1B1C1中,AA1=$\sqrt{3}$AB,四边形B1C1CB为矩形,过A1C做与直线BC1平行的平面A1CD交AB于点D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平行移动$\frac{5π}{12}$个单位长度 | B. | 向左平行移动$\frac{5π}{12}$个单位长度 | ||
| C. | 向右平行移动$\frac{5π}{6}$个单位长度 | D. | 向左平行移动$\frac{5π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
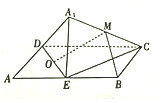 如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD).若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD).若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )| A. | 与平面A1DE垂直的直线必与直线BM垂直 | |
| B. | 过E作EG∥BM,G∈平面A1DC,则∠A1EG为定值 | |
| C. | 一定存在某个位置,使DE⊥MO | |
| D. | 三棱锥A1-ADE外接球半径与棱AD的长之比为定值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com