
���� ���������⣬�������ѡ�ֲ���ͨ����ѡ�ĸ��ʣ��Ӷ��õ���ѡ����ͨ����ѡ�ĸ��ʣ����۰�ʲô˳������ͨ����ѡ�ĸ��ʾ�Ϊ$\frac{3}{5}$��
����������ε����п���ȡֵΪ1��2��3���ֱ������Ӧ�ĸ��ʣ��ɴ�������εķֲ��к���������p1��p2��p3��ʾ�������������ѡ�ְ������IJ���˳���������������������
��� �⣺���������⣬��ѡ�ֲ���ͨ����ѡ�ĸ���Ϊ��1-$\frac{1}{5}$����1-$\frac{1}{3}$���� 1-$\frac{1}{4}$����
�ʼ�ѡ����ͨ����ѡ�ĸ���Ϊ1-��1-$\frac{1}{5}$����1-$\frac{1}{3}$���� 1-$\frac{1}{4}$��=$\frac{3}{5}$����..��3�֣�
���ı����˳�����ͨ����ѡ�ĸ���û��Ӱ�죬
��Ϊ���۰�ʲô˳���䲻��ͨ���ĸ��ʾ�Ϊ��1-$\frac{1}{5}$����1-$\frac{1}{3}$���� 1-$\frac{1}{4}$��=$\frac{2}{5}$��
�����۰�ʲô˳������ͨ����ѡ�ĸ��ʾ�Ϊ$\frac{3}{5}$����..��5�֣�
����������ε����п���ȡֵΪ1��2��3��
p����=1��=p1��
p����=2��=��1-p1�� p2��
p����=3��=��1-p1����1-p2����
�ʦεķֲ���Ϊ��
| �� | 1 | 2 | 3 |
| P | p1 | ��1-p1�� p2 | ��1-p1����1-p2�� |
���� ���⿼����ʵ���������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע������¼����ʼ��㹫ʽ�ĺ������ã�


 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д� �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
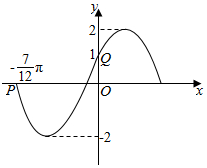 ��֪����y=Asin����x+�գ���A��0���أ�0��|��|���У���ͼ����ͼ��ʾ����ȷ���ú����Ľ���ʽ��
��֪����y=Asin����x+�գ���A��0���أ�0��|��|���У���ͼ����ͼ��ʾ����ȷ���ú����Ľ���ʽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{2}$ | B�� | 2 | C�� | $\frac{5}{2}$ | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����������P-ABC�У�PA=PB=AB=BC����PBC=90��DΪAC���е㣬AB��PD
��ͼ����������P-ABC�У�PA=PB=AB=BC����PBC=90��DΪAC���е㣬AB��PD�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 0 | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{3}$ | C�� | $\frac{2��}{3}$ | D�� | $\frac{5��}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
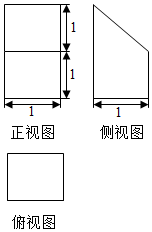
 ij�����������ͼ��ʾ��
ij�����������ͼ��ʾ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com