
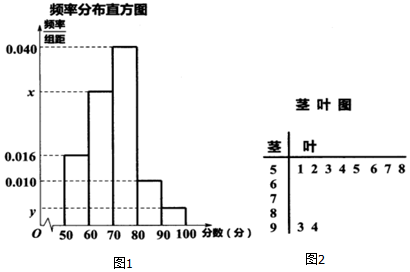
分析 (Ⅰ)由茎叶图知分值为[50,60)的人数为8人,由此能求出样本容量n和频率分布直方图中x、y的值.
(Ⅱ)[80,90)有5人,记为a,b,c,d,e,[90,100)有2人,记为f,g,随机抽取2名同学,利用列举法能求出2名同学来自不同组的概率.
解答 解:(Ⅰ)由茎叶图知分值为[50,60)的人数为8人,
则$0.016×10=\frac{8}{n}$,解得n=50,
∴$y×10=\frac{2}{50}$,解得y=0.004,
x=0.1-0.004-0.010-0.016-0.040=0.030.
(Ⅱ)[80,90)有5人,
记为a,b,c,d,e,[90,100)有2人,记为f,g,
∴随机抽取2名同学的基本事件为:
ab,ac,ad,ae,af,ag,bc,bd,be,bf,bg,cd,ce,cf,cg,de,df,dg,ef,eg,fg共21种,
2名同学来自不同组有:
af,ag,bf,bg,cf,cg,df,dg,ef,eg共10种.
∴2名同学来自不同组的概率$\frac{10}{21}$.
点评 本题考查茎叶图、频率分布直方图的应用,考查概率的求法,考查数据处理能力、运算求解能力,考查数形结合思想,是基础题.


科目:高中数学 来源: 题型:填空题
 如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,PA=PD,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l.
如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,PA=PD,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
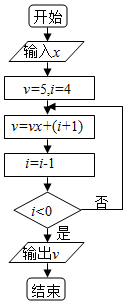 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法至今仍是比较先进的算法.如图的程序框图是针对某一多项式求值的算法,如果输入的x的值为2,则输出的v的值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法至今仍是比较先进的算法.如图的程序框图是针对某一多项式求值的算法,如果输入的x的值为2,则输出的v的值为( )| A. | 129 | B. | 144 | C. | 258 | D. | 289 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{14}$ | B. | $2\sqrt{5}$ | C. | $4\sqrt{2}$ | D. | $2\sqrt{11}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com