考点:数列递推式,数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)设b
n=a
2n-
,则
b1=a2-=-
,
=
=
,由此能证明数列{
a2n-}是以-
为首项,
为公比的等比数列.
(Ⅱ)由b
n=a
2n-
=-
•(
)
n-1=-
•(
)
n,得
a2n=-•()n+
,从而a
2n-1+a
2n=-2•(
)
n-6n+9,由此能求出S
2n.
解答:
(Ⅰ)证明:设b
n=a
2n-
,则
b1=a2-=(
a1+1)-
=-
,
=
=
=
=
,
∴数列{
a2n-}是以-
为首项,
为公比的等比数列.
(Ⅱ)解:由(Ⅰ)得b
n=a
2n-
=-
•(
)
n-1=-
•(
)
n,
∴
a2n=-•()n+
,
由a
2n=
a2n-1-3(2n-1),
得a
2n-1=3a
2n-3(2n-1)=-
•(
)
n-1-6n+
,
∴a
2n-1+a
2n=-
•[(
)
n-1+(
)
n]-6n+9
=-2•(
)
n-6n+9,
S
2n=(a
1+a
2)+(a
3+a
4)+…+(a
2n-1+a
2n)
=-2[
+()2+…+()n]-6(1+2+3+…+n)+9n
=
()n-1-3n2+6n=(
)
n-3(n-1)
2+2.
点评:本题考查等比数列的证明,考查数列的前2n项和的求法,是中档题,解题时要认真审题,注意构造法、等比数列性质、分组求和法的合理运用.



 走进文言文系列答案
走进文言文系列答案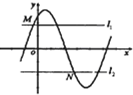 如图:M(xM,yM),N(xN,yN)分别是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与两条直线l1:y=m,l2:y=-m(A≥m≥0)的两个交点,记S=|xN-xM|,则S(m)图象大致是( )
如图:M(xM,yM),N(xN,yN)分别是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与两条直线l1:y=m,l2:y=-m(A≥m≥0)的两个交点,记S=|xN-xM|,则S(m)图象大致是( )


