
���� ��I����M�������Ϊ��12��8����������$\overrightarrow{ON}$=$\frac{3}{4}$$\overrightarrow{OM}$��������������������ɵõ�N�����꣬���������߷��̼��ɵó�p��
��II����ֱ��l1�ķ���Ϊ��x=12+m��y-8������ֱ��l2�ķ���Ϊ��x=12=$\frac{1}{m}��y-8��$���ֱ��������߷��������ɵø���ϵ���Ĺ�ϵ�������е����깫ʽ�ɵã�2=4m1���ɵ��߶�AB���е�G��2m2-8m+12��2m�����߶�DE���е�H$��\frac{2}{{m}^{2}}-\frac{8}{m}+12��\frac{2}{m}��$��ֱ��GH�ķ���Ϊ��y-2m=$\frac{m}{{m}^{2}-4m+1}$��x-2m2+8m-12�����������߷��������ɵ�my2-4��m2-4m+1��y-40m=0�����ø���ϵ���Ĺ�ϵ�ɵ��ҳ���ͨ����Ԫ���û�������ʽ�����ʡ����κ����ĵ����Լ��ɵó���
��� �⣺��I����M�������Ϊ��12��8����������$\overrightarrow{ON}$=$\frac{3}{4}$$\overrightarrow{OM}$��
��$\overrightarrow{ON}=\frac{3}{4}��12��8��=��9��6��$��
�ߵ�N����������C�ϣ���62=2p��9�����p=2��
��������C�ķ���Ϊy2=4x��
��II����ֱ��l1�ķ���Ϊ��x=12+m��y-8������ֱ��l2�ķ���Ϊ��x=12=$\frac{1}{m}��y-8��$��
����$\left\{\begin{array}{l}{x=12+m��y-8��}\\{{y}^{2}=4x}\end{array}\right.$����Ϊy2-4m1y+32m1-48=0��
��y1+y2=4m1���ɵ��߶�AB���е�G��2m2-8m+12��2m����
ͬ���ɵã��߶�DE���е�H$��\frac{2}{{m}^{2}}-\frac{8}{m}+12��\frac{2}{m}��$��
ֱ��GH�ķ���Ϊ��y-2m=$\frac{m}{{m}^{2}-4m+1}$��x-2m2+8m-12����
����$\left\{\begin{array}{l}{y-2m=\frac{m}{{m}^{2}-4m+1}��x-2{m}^{2}+8m-12��}\\{{y}^{2}=4x}\end{array}\right.$��
��Ϊmy2-4��m2-4m+1��y-40m=0��
��y1+y2=$\frac{4��{m}^{2}-4m+1��}{m}$��y1y2=-40��
���ҳ�=$\sqrt{��1+\frac{��{m}^{2}-4m+1��^{2}}{{m}^{2}}��[\frac{16��{m}^{2}-4m+1��^{2}}{{m}^{2}}+160]}$��
��ֱ��l1����б����[$\frac{��}{6}$��$\frac{��}{4}$]��ʱ��б��k��$[\frac{\sqrt{3}}{3}��1]$��m��$[1��\sqrt{3}]$��
��$��\frac{{m}^{2}-4m+1}{m}��^{2}$=t��
��t=$��m+\frac{1}{m}-4��^{2}$�ܣ�2-4��2=4��
���ҳ���$\sqrt{��1+4��[4��16+160]}$=$4\sqrt{70}$��
�൱m=1����l1����б��Ϊ$\frac{��}{4}$ʱ���ҳ�ȡ�����ֵΪ��4$\sqrt{70}$��
���� ���⿼���������ߵı����̼������ʡ�ֱ�����������ཻ����ת��Ϊ���������ɵø���ϵ���Ĺ�ϵ���ҳ���ʽ����������ʽ�����ʡ����κ����ĵ����ԡ��������������㣬�����˻�Ԫ��������������������������������������⣮


 ��ҵ����ϵ�д�
��ҵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij��ҵ�⽨����ͼ��ʾ�����������ƺ�ȣ����ȵ�λ���ף��������������м�ΪԲ���Σ��������˾�Ϊ�����Σ��������Ҫ�����������Ϊ$\frac{80��}{3}$�����ף���l��2r������������Ľ�����ý����������йأ���֪Բ���β���ÿƽ���������Ϊ3ǧԪ�������β���ÿƽ���������Ϊc��c��5��ǧԪ����������Ľ������ΪyǧԪ��
ij��ҵ�⽨����ͼ��ʾ�����������ƺ�ȣ����ȵ�λ���ף��������������м�ΪԲ���Σ��������˾�Ϊ�����Σ��������Ҫ�����������Ϊ$\frac{80��}{3}$�����ף���l��2r������������Ľ�����ý����������йأ���֪Բ���β���ÿƽ���������Ϊ3ǧԪ�������β���ÿƽ���������Ϊc��c��5��ǧԪ����������Ľ������ΪyǧԪ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
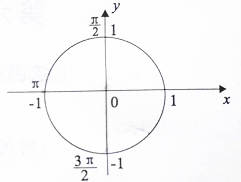 ��λԲ�����Ǻ���ֵ�ļ��Ͻ����ǡ����ڻ��ϣ�ֵ�����ϡ�������ͼ�л��������ڵڢ�����һ������ֵ������ֵ��
��λԲ�����Ǻ���ֵ�ļ��Ͻ����ǡ����ڻ��ϣ�ֵ�����ϡ�������ͼ�л��������ڵڢ�����һ������ֵ������ֵ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com