
【题目】已知函数![]() ,其中e是自然对数的底数.
,其中e是自然对数的底数.
(1)若![]() ,证明:
,证明:![]() ;
;
(2)若![]() 时,都有
时,都有![]() ,求实数a的取值范围.
,求实数a的取值范围.
【答案】(1)证明见解析(2)![]()
【解析】
(1)当![]() 时,
时,![]() ,利用导数求出函数
,利用导数求出函数![]() 的单调区间并求出最小值,即可证明
的单调区间并求出最小值,即可证明![]() ;
;
(2)令![]() ,由
,由![]() 时,都有
时,都有![]() ,可得
,可得![]() 在
在![]() 上恒成立,利用导数判断
上恒成立,利用导数判断![]() 在
在![]() 的单调性,分别讨论
的单调性,分别讨论![]() 和
和![]() 两种情况,即可得到
两种情况,即可得到![]() 的取值范围.
的取值范围.
(1)由题意,当![]() 时,
时,![]() ,
,
所以![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
所以![]() 在
在![]() 时取得极小值,也是最小值.
时取得极小值,也是最小值.
所以![]() .
.
(2)令![]() ,
,![]() ,
,
由![]() 时,都有
时,都有![]() ,所以
,所以![]() 在
在![]() 上恒成立.
上恒成立.
由![]() ,令
,令![]() ,
,
则![]() 在
在![]() 上恒成立.
上恒成立.
所以![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
①当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() ,满足题意.
,满足题意.
②当![]() 时,因为
时,因为![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,
,
存在![]() ,使得当
,使得当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
所以当![]() 时,
时,![]() ,这与
,这与![]() 在
在![]() 上恒成立矛盾.
上恒成立矛盾.
综上所述,![]() ,即实数a的取值范围
,即实数a的取值范围![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】数学与文学之间存在着奇妙的联系,诗中有回文诗,如“山东落花生花落东山,西湖回游鱼游回湖西”,倒过来读,仍然是原句!数学上也有这样一类数,如66,202,3773,34543,无论从左往右读,还是从右往左读,都是同一个数,我们称这样的数为“回文数”,现用数字1,2,3,4组数(可重复用),则组成的五位“回文数”的个数为( )
A.24B.28C.48D.64
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的准线经过点
的准线经过点![]() ,过
,过![]() 的焦点
的焦点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,则下列结论正确的是( )
两点,则下列结论正确的是( )
A.![]() B.
B.![]() 的最小值为16
的最小值为16
C.四边形![]() 的面积的最小值为64D.若直线
的面积的最小值为64D.若直线![]() 的斜率为2,则
的斜率为2,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在党中央的英明领导下,在全国人民的坚定支持下,中国的抗击“新型冠状肺炎”战役取得了阶段性胜利,现在摆在我们大家面前的是有序且安全的复工复产.某商场为了提振顾客的消费信心,对某中型商品实行分期付款方式销售,根据以往资料统计,顾客购买该商品选择分期付款的期数ξ的分布列为

其中0<a<1,0<b<1.
(1)求购买该商品的3位顾客中,恰有1位选择分4期付款的概率;
(2)商场销售一件该商品,若顾客选择分4期付款,则商场获得的利润为2000元;若顾客选择分5期付款,则商场获得的利润为2500元;若顾客选择分6期付款,则商场获得的利润为3000元,假设该商场销售两件该商品所获得的利润为X(单位:元),
(i)设X=5500时的概率为m,求当m取最大值时,利润X的分布列和数学期望;
(ii)设某数列{xn}满足x1=0.4,xn=a,2xn+1=b,若a<0.25,求n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的两焦点之间的距离为2,两条准线间的距离为8,直线l:y=k(x-m)(m∈R)与椭圆交于P,Q两点.
=1(a>b>0)的两焦点之间的距离为2,两条准线间的距离为8,直线l:y=k(x-m)(m∈R)与椭圆交于P,Q两点.
(1) 求椭圆C的方程;
(2) 设椭圆的左顶点为A,记直线AP,AQ的斜率分别为k1,k2.①若m=0,求k1k2的值;②若k1k2=-![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位战士参加射击比赛训练.从若干次预赛成绩中随机抽取8次,记录如下:
甲82 81 79 78 95 88 93 84
乙92 95 80 75 83 80 90 85
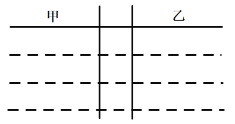
(1)用茎叶图表示这两组数据,并分别求两组数据的中位数;
(2)现要从中选派一人参加射击比赛,从统计学的角度考虑,你认为选派哪位战士参加合适?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax+blnx(a,b∈R),曲线y=f(x)在点(1,f(1))处的切线方程为2x﹣y﹣2=0.
(1)判断f(x)在定义域内的单调性,并说明理由;
(2)若对任意的x∈(1,+∞),不等式f(x)≤m(ex﹣1﹣1)恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,圆
,圆![]() :
:![]() ,动圆
,动圆![]() 与圆
与圆![]() 和圆
和圆![]() 均内切.
均内切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,过点
两点,过点![]() 且垂直于
且垂直于![]() 的直线交轨迹
的直线交轨迹![]() 于两点
于两点![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com