
| A. | a=$\frac{1}{2}$ | B. | a>1或a=$\frac{1}{2}$ | C. | $\frac{1}{2}$≤a<1 | D. | $\frac{1}{2}$<a<1 |
分析 将曲线y=$\sqrt{a-{x}^{2}}$(a>0)看成一个半圆,画出直线x+y=1与半圆恰有一个公共点时的情况,求解a的取值范围即可.
解答 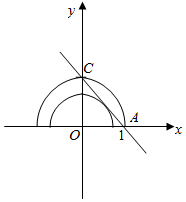 解:由曲线y=$\sqrt{a-{x}^{2}}$(a>0),知y≥0,
解:由曲线y=$\sqrt{a-{x}^{2}}$(a>0),知y≥0,
等式两边同时平方,整理可得x2+y2=a2,
即曲线y=$\sqrt{a-{x}^{2}}$(a>0)是以(0,0)点为圆心,以$\sqrt{a}$为半径的半圆(y≥0)
已知直线x+y=1,可在直角坐标系中给出图象(如下图)
由图象可知,当半圆的半径$\sqrt{a}$>1即a>1时或者半圆与直线相切时恰有一个公共交点,
当半圆与直线相切时,圆心(0,0)到直线的距离即为半圆的半径,此时$\sqrt{a}$$\frac{|-1|}{\sqrt{2}}$,即a=$\frac{1}{2}$
所以当直线x+y=1与曲线y=$\sqrt{a-{x}^{2}}$(a>0)恰有一个公共点时,a的取值范围是a=$\frac{1}{2}$或a>1.
故选:B.
点评 对于直线和圆的交点个数问题,采用数形结合的思想来考虑较为直观、简单.是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
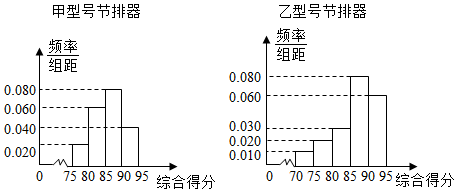
| 综合得分k的取值范围 | 节排器等级 | 节排器利润率 |
| k≥85 | 一级品 | a |
| 75≤k<85 | 二级品 | 5a2 |
| 70≤k<75 | 三级品 | a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2}{3}$,1] | B. | [1,9] | C. | [$\frac{2}{3}$,9] | D. | [$\frac{\sqrt{6}}{3}$,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com