练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=3，且$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影与$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影相等，则|$\overrightarrow{a}$-$\overrightarrow{b}$|等于（　　）
    A．$\sqrt{2}$B．$\sqrt{10}$C．2$\sqrt{2}$D．2

    分析 由题意由于$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影与$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影相等，由此可以求出这两个向量的加角，又向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=3，|$\overrightarrow{a}$-$\overrightarrow{b}$|2=（$\overrightarrow{a}$-$\overrightarrow{b}$）2利用向量的运算规律既可以求解

    解答 解：因为由于$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影与$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影相等，设这两个向量的夹角为θ，则|$\overrightarrow{a}$|cosθ=|$\overrightarrow{b}$|cosθ?1cosθ=3cosθ⇒cosθ=0，所以θ=$\frac{π}{2}$，
    又由于，|$\overrightarrow{a}$-$\overrightarrow{b}$|2=（$\overrightarrow{a}$-$\overrightarrow{b}$）2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2-2$\overrightarrow{a}•\overrightarrow{b}$=1+9=10；
    所以|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{10}$；
    故选：B．

    点评 本题考查了向量的投影，向量的模及向量的数量积的运算规律．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=ln（ax+1）+$\frac{2}{x+1}$-1（x≥0，a＞0）．求f（x）的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．某几何体的三视图如图所示，且该几何体的体积是3，则该几何体的所有棱中，最长的棱为（　　）
    A．$\sqrt{13}$B．$\sqrt{5}$C．$\sqrt{14}$D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．在数列{an}中，已知a1=2，a2=7，an+2等于anan+1（n∈N+）的个位数，则a2015=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．某同学在篮球场上进行投篮训练，先投“2分的篮”2次，每次投中的概率为$\frac{4}{5}$，每投中一次得2分，不中得0分；再投“3分的篮”1次，每次投中的概率为$\frac{2}{3}$，投中得3分，不中得0分，该同学每次投篮的结果相互独立，假设该同学要完成以上三次投篮．
    （Ⅰ）求该同学恰好2次投中的概率；
    （Ⅱ）求该同学所得分X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．在边长为1的正三角形ABC中任取一点M，则AM＜$\frac{\sqrt{3}}{2}$的概率为（　　）
    A．$\frac{\sqrt{3}π}{18}$B．$\frac{\sqrt{3}π}{12}$C．$\frac{\sqrt{3}π}{9}$D．$\frac{\sqrt{3}π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．将函数f（x）=$\sqrt{3}$cos2$\frac{x}{2}$+$\frac{1}{2}$sinx-$\frac{\sqrt{3}}{2}$的图象上所有点的纵坐标不变，横坐标变为原来的$\frac{1}{2}$，再将所得图象向右平移$\frac{π}{3}$得到函数g（x），则函数g（x）的解析式为（　　）
    A．g（x）=cos$\frac{x}{2}$B．g（x）=-sin2xC．g（x）=sin（2x-$\frac{π}{3}$）D．g（x）=sin（$\frac{x}{2}$+$\frac{π}{6}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知复数z：满足（1+$\sqrt{3}$i）z=1+i，则|z|等于（　　）
    A．$\frac{\sqrt{2}}{2}$B．-$\sqrt{2}$C．$\sqrt{2}$D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

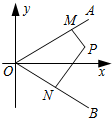    5．如图，射线OA，OB所在的直线的方向向量分别为$\overrightarrow{d_1}=（{1，k}）$，$\overrightarrow{d_2}=（{1，-k}）（{k＞0}）$，点P在∠AOB内，PM⊥OA于M，PN⊥OB于N；
    （1）若k=1，$P（{\frac{3}{2}，\frac{1}{2}}）$，求|OM|的值；
    （2）若P（2，1），△OMP的面积为$\frac{6}{5}$，求k的值；
    （3）已知k为常数，M，N的中点为T，且${S_{△MON}}=\frac{1}{k}$，当P变化时，求|OT|的取值范围．

    查看答案和解析>>

    同步练习册答案