
分析 根据题意,对于数列{an},设其首项为a1,公比为q,结合题意可得$\left\{\begin{array}{l}{{a}_{1}q+{a}_{1}{q}^{3}=10}\\{{a}_{1}•{a}_{1}{q}^{4}=16}\end{array}\right.$,解可得等比数列的首项与公比,由等比数列前n项和公式计算可得答案.
解答 解:根据题意,对于数列{an},设其首项为a1,公比为q,
又由a2+a4=10,a1.a5=16,
又{an}是递增数列,
则有$\left\{\begin{array}{l}{{a}_{1}q+{a}_{1}{q}^{3}=10}\\{{a}_{1}•{a}_{1}{q}^{4}=16}\end{array}\right.$,
解可得a1=1,q=2,
则其前6项和S6=$\frac{1×(1-{2}^{6})}{1-2}$=63;
故答案为:63.
点评 本题考查等比数列的前n项和,关键是依据题意求出等比数列的首项与公比.


科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (2,3) | C. | (2,3] | D. | [-1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤0 | B. | 0$≤a≤\frac{3}{5}$ | C. | a≤$\frac{3}{5}$ | D. | a≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
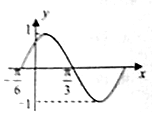 函数f(x)=sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1+x2=$\frac{2π}{3}$,则f(x1)+f(x2)=( )
函数f(x)=sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1+x2=$\frac{2π}{3}$,则f(x1)+f(x2)=( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5050 | B. | 5100 | C. | 9800 | D. | 9850 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a | B. | $-\frac{1}{4}a$ | C. | $\frac{1}{4}a$ | D. | -a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | Ⅰ | B. | Ⅱ | C. | Ⅲ | D. | Ⅳ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com